Observateurs d’état et filtres de Kalman
Les observateurs d’état combinent des informations sur le comportement d’un système et des mesures externes pour estimer l’état du système. Un observateur commun utilisé pour les systèmes linéaires est le filtre de Kalman. Les filtres de Kalman sont avantageux par rapport aux autres filtres car ils fusionnent les mesures d’un ou plusieurs capteurs avec un modèle d’espace d’état du système pour estimer de manière optimale l’état d’un système.
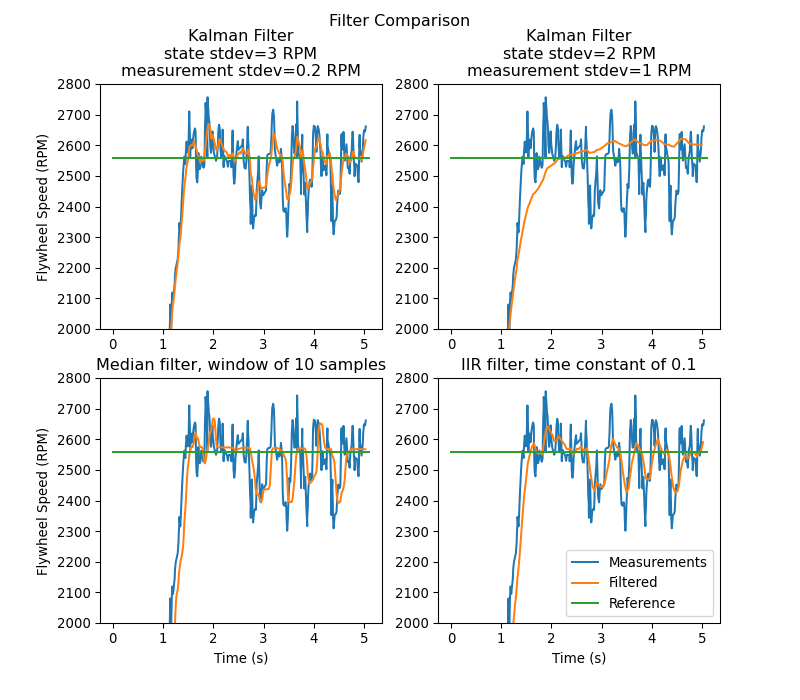
Cette image montre les mesures de vitesse d’un volant d’inertie au fil du temps, exécutées à travers une variété de filtres différents. Notez qu’un filtre de Kalman bien réglé ne montre aucun décalage de mesure pendant la rotation du volant tout en rejetant les données bruyantes et en réagissant rapidement aux perturbations lorsque les billes le traversent. Vous trouverez plus d’informations sur les filtres dans la :ref:` section filtres <docs/software/advanced-controls/filters/index:Filters>`.
Les fonctions gaussiennes
Kalman filters utilize a Gaussian distribution to model the noise in a process [1]. In the case of a Kalman filter, the estimated state of the system is the mean, while the variance is a measure of how certain (or uncertain) the filter is about the true state.
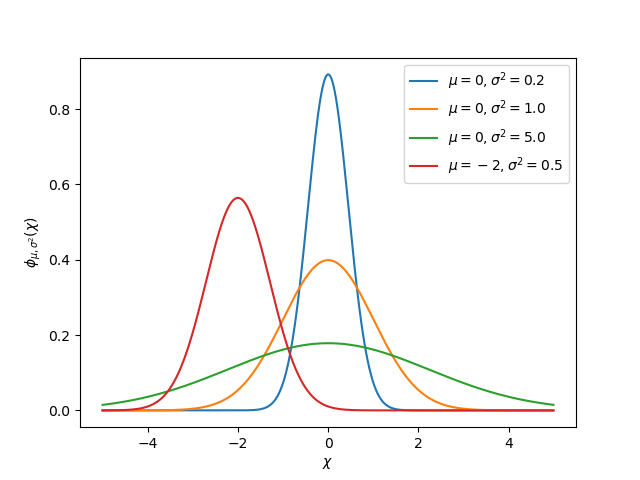
L’idée de variance et de covariance est au cœur de la fonction d’un filtre de Kalman. La covariance est une mesure de la manière dont deux variables aléatoires sont corrélées. Dans un système à un seul état, la matrice de covariance est simplement \(\mathbf{\text{cov}(x_1, x_1)}\), ou une matrice contenant la variance \(\mathbf{\text{var}(x_1)}\) de l’état \(x_1\). L’amplitude de cette variance est le carré de l’écart type de la fonction gaussienne décrivant l’estimation de l’état actuel. Des valeurs relativement élevées de covariance peuvent indiquer des données bruyantes, tandis que de petites covariances peuvent indiquer que le filtre est plus sûr de son estimation. Rappelez-vous que les valeurs « grandes » et « petites » de la variance ou de la covariance sont relatives à l’unité de base utilisée - par exemple, si \(\mathbf{x_1}\) a été mesurée en mètres, \(\mathbf{\text{cov}(x_1, x_1)}\) serait en mètres carrés.
Les matrices de covariance sont écrites sous la forme suivante:
Les filtres de Kalman
Important
Il est important de développer une intuition de ce que fait réellement un filtre de Kalman. Le livre Kalman and Bayesian Filters in Python par Roger Labbe fournit une excellente introduction visuelle et intéractive aux filtres bayésiens. Les filtres de Kalman de la WPILib utilisent l’algèbre linéaire pour rendre plus accessible les mathématiques, mais les idées sont similaires au cas unidimensionnel. Nous vous suggérons de lire le chapitre 4 pour avoir une idée de ce que font ces filtres.
To summarize, Kalman filters (and all Bayesian filters) have two parts: prediction and correction. Prediction projects our state estimate forward in time according to our system’s dynamics, and correct steers the estimated state towards the measured state. While filters often perform both in the same timestep, it’s not strictly necessary – For example, WPILib’s pose estimators call predict frequently, and correct only when new measurement data is available (for example, from a low-framerate vision system).
Ce qui suit montre les équations d’un filtre de Kalman à temps discret:
L’estimation d’état \(\mathbf{x}\), avec \(\mathbf{P}\), décrivent la moyenne et la covariance de la fonction gaussienne qui décrit l’estimation par notre filtre de l’état réel du système.
Les matrices de covariance du bruit de processus et de mesure
Les matrices de covariance du bruit de processus et de mesure \(\mathbf{Q}\) et \(\mathbf{R}\) décrivent la variance de chacun de nos états et mesures. N’oubliez pas que pour une fonction gaussienne, la variance est le carré de l’écart type de la fonction. Dans un WPILib, Q et R sont des matrices diagonales dont les diagonales contiennent leurs variances respectives. Par exemple, un filtre de Kalman avec les états \(\begin{bmatrix}\text{position} \\ \text{velocity} \end{bmatrix}\) et les mesures \(\begin{bmatrix}\text{position} \end{bmatrix}\) avec les écarts-types d’état \(\begin{bmatrix}0.1 \\ 1.0\end{bmatrix}`et l'écart-type de mesure :math:\)begin{bmatrix}0.01end{bmatrix}` aurait les matrices suivantes \(\mathbf{Q}\) et \(\mathbf{R}\) :
Matrice de covariance d’erreur
La matrice de covariance d’erreur \(\mathbf{P}\) décrit la covariance de l’estimation d’état \(\mathbf{\hat{x}}\). De manière informelle, \(\mathbf{P}\) décrit notre certitude quant à l’état estimé. Si \(\mathbf{P}\) est grand, notre incertitude sur l’état vrai est grande. Inversement, un \(\mathbf{P}\) avec des éléments plus petits impliquerait moins d’incertitude sur notre véritable état.
Au fur et à mesure que nous projetons le modèle vers l’avant, \(\mathbf{P}\) augmente à mesure que notre certitude sur l’état réel du système diminue.
L’étape de prédiction
En prédiction, notre estimation d’état est mise à jour selon la dynamique du système linéaire \(\mathbf{\dot{x} = Ax + Bu}\). De plus, notre covariance d’erreur \(\mathbf{P}\) augmente selon la matrice de covariance du bruit de processus \(\mathbf{Q}\). Des valeurs plus grandes de:math:mathbf{Q} feront croître notre covariance d’erreur \(\mathbf{P}\) plus rapidement. Ceci \(\mathbf{P}\) est utilisé dans l’étape de correction pour pondérer le modèle et les mesures.
L’étape correcte
À l’étape correcte, notre estimation d’état est mise à jour pour inclure de nouvelles informations de mesure. Cette nouvelle information est pondérée par rapport à l’estimation d’état \(\mathbf{\hat{x}}\) par le gain de Kalman \(\mathbf{K}\). Les grandes valeurs de \(\mathbf{K}\) influencent plus fortement les mesures entrantes, tandis que les valeurs plus petites de \(\mathbf{K}\) influencent plus fortement notre prédiction d’état. Parce que \(\mathbf{K}\) est lié à \(\mathbf{P}\), des valeurs plus grandes de \(\mathbf{P}\) augmenteront \(\mathbf{K}\) et influencer encore plus les mesures. Si, par exemple, un filtre est utilisé pour une longue période, une valeur élevée de \(\mathbf{P}\) pondérerait fortement les nouvelles informations.
Enfin, la covariance d’erreur \(\mathbf{P}\) diminue pour augmenter notre confiance dans l’estimation de l’état.
Le réglage des filtres Kalman
Les constructeurs des classes de filtre Kalman de WPILib utilisent un système linéaire, un vecteur des écarts-types de bruit de processus et des écarts-types de bruit de mesure. Ceux-ci sont convertis en matrices \(\mathbf{Q}\) et \(\mathbf{R}\) en remplissant les diagonales avec le carré des écarts-types, ou variances, de chaque état ou mesure. En diminuant l’écart type d’un état (et donc son entrée correspondante dans \(\mathbf{Q}\)), le filtre se fera moins confiance aux mesures entrantes. De même, l’augmentation de l’écart type d’un état fera davantage confiance aux mesures entrantes. Il en va de même pour les écarts-types de mesure - la diminution d’une entrée augmentra la confiance du filtre par rapport à la mesure entrante pour l’état correspondant, tandis que son augmentation diminuera la confiance dans la mesure.
48 // The observer fuses our encoder data and voltage inputs to reject noise.
49 private final KalmanFilter<N1, N1, N1> m_observer =
50 new KalmanFilter<>(
51 Nat.N1(),
52 Nat.N1(),
53 m_flywheelPlant,
54 VecBuilder.fill(3.0), // How accurate we think our model is
55 VecBuilder.fill(0.01), // How accurate we think our encoder
56 // data is
57 0.020);
5#include <numbers>
6
7#include <frc/DriverStation.h>
8#include <frc/Encoder.h>
9#include <frc/TimedRobot.h>
10#include <frc/XboxController.h>
11#include <frc/controller/LinearQuadraticRegulator.h>
12#include <frc/drive/DifferentialDrive.h>
13#include <frc/estimator/KalmanFilter.h>
14#include <frc/motorcontrol/PWMSparkMax.h>
15#include <frc/system/LinearSystemLoop.h>
16#include <frc/system/plant/DCMotor.h>
17#include <frc/system/plant/LinearSystemId.h>
18#include <units/angular_velocity.h>
48 // The observer fuses our encoder data and voltage inputs to reject noise.
49 frc::KalmanFilter<1, 1, 1> m_observer{
50 m_flywheelPlant,
51 {3.0}, // How accurate we think our model is
52 {0.01}, // How accurate we think our encoder data is
53 20_ms};
48 # The observer fuses our encoder data and voltage inputs to reject noise.
49 self.observer = wpimath.estimator.KalmanFilter_1_1_1(
50 self.flywheelPlant,
51 [3], # How accurate we think our model is
52 [0.01], # How accurate we think our encoder data is
53 0.020,
54 )