Introduction au Contrôle de l’Espace-État
Note
Cet article est tiré de Controls Engineering in FRC par Tyler Veness avec permission.
Du PID au Contrôle à base d’un modèle
Quand nous réglons les contrôleurs PID, nous nous concentrons le réglage des paramètres du contrôleur liés à l’erreur actuel, du passé et du futur. (termes P, I et D) au lieu de nous concentrer aux états du système sous-jacent. Bien que cette approche fonctionne dans beaucoup de situations, c’est une vue incomplète de la réalité du système étudié.
Le contrôle à partir d’un modèle se concentre sur le développement d’un modèle précis du système (mécanisme) que nous essayons de contrôler. Ces modèles aident à affiner les gains choisis pour les commandes de rétroaction basées sur les réponses phyiques du système, au lieu d’avoir un gain proportionnel arbitraire dérivé de tests. Cela nous permet non seulement de prédire comment un système va réagir, mais aussi de tester nos contrôleurs sans avoir un robot physique en notre possession et gagner du temps pendant le débogage des simples bogues .
Note
State-space control makes extensive use of linear algebra. More on linear algebra in modern control theory, including an introduction to linear algebra and resources, can be found in Chapter 5 of Controls Engineering in FRC.
Si vous avez utilisé les classes feedforward de WPILib pour SimpleMotorFeedforward ou ses classes sœurs, ou utilisé SysId pour choisir PID gains `<gain> pour vous, vous êtes déjà familiarisé avec le contrôle basé sur un modèle ! Les ``kv` et ka gains `<gain> peuvent être utilisés pour décrire comment un moteur (ou un bras, ou une transmission) réagira à la tension. Nous pouvons mettre ces constantes dans la notation d’espace d’état standard en utilisant le ``LinearSystem` de WPILib, ce que nous ferons dans un article ultérieur.
Vocabulaire
Pour le vocabulaire de base qui sera utilisé tout au long de cet article, consultez le Glossaire.
Introduction à l’algèbre linéaire
Pour une courte et intuitive introduction aux concepts de base de l’algèbre linéaire, nous vous recommandons les chapitres 1 à 4 de la série Essence of Linear Algebra par 3Blue1Brown (Vecteurs, qu’est-ce même?, Combinaisons linéaires, couverture, vecteurs de base, transformations linéaires et matrices, et multiplication de matrices comme composition).
Qu’est-ce que c’est que l’espace-état?
Recall that 2D space has two axes: x and y. We represent locations within this space as a pair of numbers packaged in a vector, and each coordinate is a measure of how far to move along the corresponding axis. State-space is a Cartesian coordinate system with an axis for each state variable, and we represent locations within it the same way we do for 2D space: with a list of numbers in a vector. Each element in the vector corresponds to a state of the system. This example shows two example state vectors in the state-space of an elevator model with the states \([\text{position}, \text{velocity}]\):
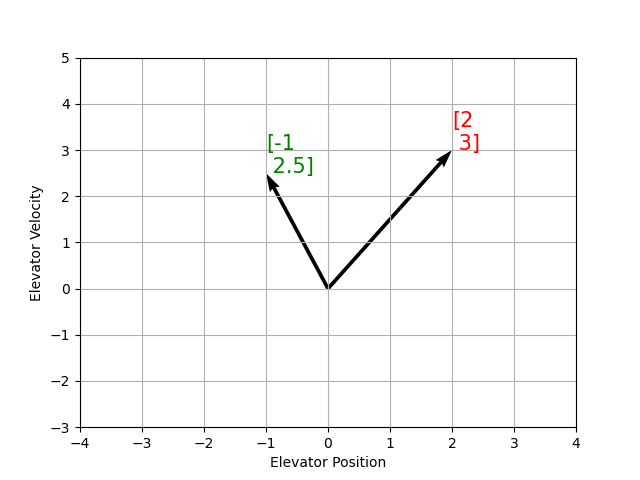
Dans cette image, les vecteurs qui représentent les états dans l’espace-état sont des flèches. À partir de maintenant ces vecteurs seront représentés simplement par un point à la pointe du vecteur, mais souvenez-vous que le reste du vecteur est toujours là.
En plus de l’état, les entrées et sorties sont representées aussi comme des vecteurs. Puisque la correspondance des états actuels et les entrées au changement de l’état est un système d’équations, c’est naturel d’écrire cette relation sous forme de matrice. Cette équation matricielle peut être écrite dans notation d’espace-état.
Qu’est-ce que c’est que la notation espace-état?
La notation espace-état est un ensemble d’équations matricielles qui décrit comment un système évoluera dans le temps. Ces équations relient le changement de l’état \(\dot{\mathbf{x}}\), et la sortie \(\mathbf{y}\), à des combinaisons linéaires du vecteur d’état actuel \(\mathbf{x}\) et le vecteur d’entrée \(\mathbf{u}\).
Le contrôle de l’espace-état peut traiter des systèmes en temps continu ou en temps discret. Dans le cas du temps continu, le taux de variation de l’état du système \(\mathbf{\dot{x}}\) est exprimé comme une combinaison linéaire de l’état courant \(\mathbf{x}\) et de l’entrée \(\mathbf{u}\).
En revanche, les systèmes à temps discret expriment l’état du système à notre prochain pas de temps \(\mathbf{x}_{k+1}\) basé sur l’état actuel \(\mathbf{x}_k\) et l’entrée \(\mathbf{u}_k\), où \(k\) est le pas de temps actuel et \(k+1\) est le prochain pas de temps.
Dans les deux formes de temps continu et discret, le vecteur de sortie \(\mathbf{y}\) est exprimé comme une combinaison linéaire de l’état actuel et de l’entrée. Dans de nombreux cas, la sortie est un sous-ensemble de l’état du système et n’a aucune contribution de l’entrée actuelle.
Lors de la modélisation de systèmes, nous dérivons d’abord la représentation en temps continu parce que les équations de mouvement sont naturellement écrites comme le taux de changement de l’état d’un système comme une combinaison linéaire de son état actuel et des entrées. Nous convertissons cette représentation en temps discret sur le robot parce que nous mettons à jour le système par intervalles de temps discrets au lieu de le faire en continu.
Les deux ensembles d’équations suivantes constituent la forme standard de notation espace-état en temps continu et en temps discret :
Un système d’espace d’état à temps continu peut être converti en un système à temps discret grâce à un processus appelé discrétisation.
Note
Dans la forme à temps discret, l’état du système est maintenu constant entre les mises à jour. Cela signifie que nous ne pouvons réagir aux perturbations aussi rapidement que notre estimation d’état est mise à jour. Mettre à jour notre estimation plus rapidement peut aider à améliorer les performances, jusqu’à un certain point. La classe Notifier de WPILib peut être utilisée si des mises à jour plus rapides que la boucle principale du robot sont souhaitées.
Note
Bien que les matrices en temps continu et en temps discret A, B, C et D d’un système portent les mêmes noms, elles ne sont pas équivalentes. Les matrices à temps continu décrivent le taux de changement de l’état, \(\mathbf{x}\), tandis que les matrices à temps discret décrivent l’état du système au prochain intervalle de temps en fonction de l’état actuel et de l’entrée.
Important
LinearSystem de WPILib prend des matrices système en temps continu et les convertit en interne en forme de temps discret si nécessaire.
State-space Notation Example: Flywheel from Kv and Ka
Recall that we can model the motion of a flywheel connected to a brushed DC motor with the equation \(V = K_v \cdot v + K_a \cdot a\), where V is voltage output, v is the flywheel’s angular velocity and a is its angular acceleration. This equation can be rewritten as \(a = \frac{V - K_v \cdot v}{K_a}\), or \(a = \frac{-K_v}{K_a} \cdot v + \frac{1}{K_a} \cdot V\). Notice anything familiar? This equation relates the angular acceleration of the flywheel to its angular velocity and the voltage applied.
Nous pouvons convertir cette équation en notation d’espace d’états. Nous pouvons créer un système avec un état (vitesse), une entrée (tension), et une sortie (vitesse). En rappelant que la première dérivée de la vitesse est l’accélération, nous pouvons écrire notre équation comme suit, en remplaçant la vitesse par \(\mathbf{x}\), l’accélération par \(\mathbf{\dot{x}}\), et la tension \(\mathbf{V}\) par \(\mathbf{u}\):
The output and state are the same, so the output equation is the following:
That’s it! That’s the state-space model of a system for which we have the \(K_v\) and \(K_a\) constants. This same math is used in system identification to model flywheels and drivetrain velocity systems.
Visualisation des réponses de l’espace d’état: portrait de phase
A phase portrait can help give a visual intuition for the response of a system in state-space. The vectors on the graph have their roots at some point \(\mathbf{x}\) in state-space, and point in the direction of \(\mathbf{\dot{x}}\), the direction that the system will evolve over time. This example shows a model of a pendulum with the states of angle and angular velocity.
Pour tracer une trajectoire potentielle qu’un système pourrait emprunter à travers l’espace d’états, choisissez un point de départ et suivez les flèches. Dans cet exemple, nous pourrions commencer par \([-2, 0]\). À partir de là, la vitesse augmente à mesure que nous nous balançons verticalement et commence à diminuer jusqu’à ce que nous atteignions l’extrême opposé du balancement. Ce cycle de rotation autour de l’origine se répète indéfiniment.
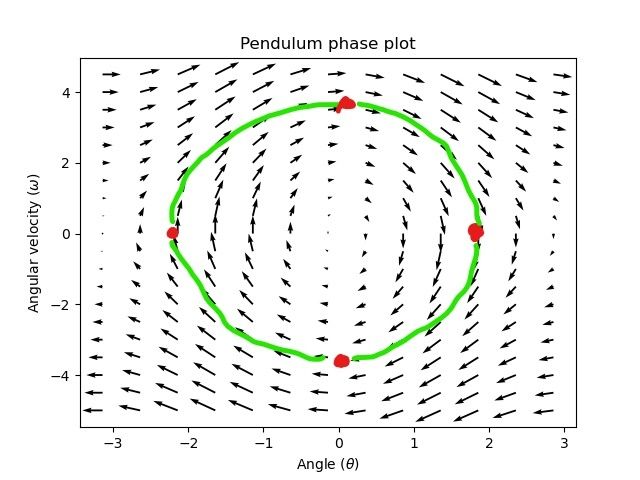
Notez que près des bords du portrait de phase, l’axe X s’enroule comme une rotation de \(\pi\) radians dans le sens antihoraire et une rotation de \(\pi\) radians dans le sens horaire se terminera au même point.
Pour en savoir plus sur les équations différentielles et les portraits de phase, voir la vidéo sur les équations différentielles de 3Blue1Brown – ils font un excellent travail d’animation de l’espace de phase du pendule vers 15:30 minutes après le début du vidéo.
Visualiser le Feedforward
Ce portrait de phase montre les réponses « en boucle ouverte » du système - c’est-à-dire comment il réagira si nous laissons l’état évoluer naturellement. Si nous voulons, par exemple, équilibrer le pendule horizontal (à \((\frac{\pi}{2}, 0)\) dans l’espace d’états), nous aurions besoin d’appliquer une commande d’entrée pour contrer la tendance en boucle ouverte du pendule à basculer vers le bas. C’est ce que la commande prédictive essaie de faire - faire en sorte que notre portrait de phase ait un équilibre à la position de référence (ou point de consigne) dans l’espace d’états.
Looking at our phase portrait from before, we can see that at \((\frac{\pi}{2}, 0)\) in state space, gravity is pulling the pendulum down with some torque T, and producing some downward angular acceleration with magnitude \(\frac{\tau}{I}\), where I is angular moment of inertia of the pendulum. If we want to create an equilibrium at our reference of \((\frac{\pi}{2}, 0)\), we would need to apply an input can counteract the system’s natural tendency to swing downward. The goal here is to solve the equation \(\mathbf{0 = Ax + Bu}\) for \(\mathbf{u}\). Below is shown a phase portrait where we apply a constant input that opposes the force of gravity at \((\frac{\pi}{2}, 0)\):
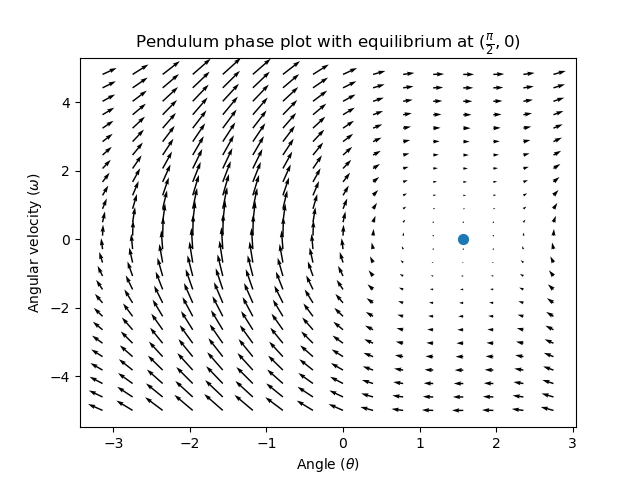
Commande de rétroaction
Dans le cas d’un moteur à courant continu, avec juste un modèle mathématique et une connaissance de tous les états actuels du système (c’est-à-dire la vitesse angulaire), nous pouvons prédire tous les états futurs compte tenu des futures entrées de tension. Mais si le système est perturbé d’une manière qui n’est pas modélisée par nos équations, comme une charge ou un frottement inattendu, la vitesse angulaire du moteur s’écartera du modèle au fil du temps. Pour lutter contre cela, nous pouvons donner au moteur des commandes correctives à l’aide d’un contrôleur de rétroaction.
Un contrôleur PID est une forme de commande de rétroaction. Le contrôle de l’espace d’états utilise souvent la loi de commande suivante, où \(\mathbf{K}\) est la matrice de gain d’une commande, \(\mathbf{r}\) est l’état de référence, et \(\mathbf{x}\) est l’état actuel dans l’espace d’états. La différence entre ces deux vecteurs, \(\mathbf{r-x}\), correspond à l’erreur.
Cette loi de commande correspond à un contrôleur proportionnel pour chaque état de notre système. Les contrôleurs proportionnels créent des « ressorts » définis par logiciel qui tirent l’état de notre système vers notre état de référence dans l’espace d’états. Dans le cas où le système commandé a des états de position et de vitesse, la loi de commande ci-dessus se comportera comme un contrôleur PD, qui essaie également de ramener l’erreur de position et de vitesse à zéro.
Montrons un exemple de cette loi de commande en action. Nous utiliserons le système de pendule décrit plus haut, où le pendule oscillant encercle l’origine dans l’espace d’états. Le cas où \(\mathbf {K}\) est la matrice nulle (une matrice dont tous les éléments sont des zéros) équivaut à choisir des gains P et D nuls - aucune entrée de commande serait appliquée, et le diagramme de phase serait identique à celui présenté ci-dessus.
Pour ajouter une rétroaction, nous choisissons arbitrairement un \(\mathbf {K}\) de [2, 2], où notre entrée du pendule est une accélération angulaire. Ce K signifie que pour chaque erreur de position de 1 radian, l’accélération angulaire serait de 2 radians par seconde au carré; en d’autres mots, nous accélérons de 2 radians par seconde au carré pour chaque radian par seconde term:d’erreur. Essayez de suivre une flèche en provenance de quelque part dans l’espace d’états vers l’intérieur - quelles que soient les conditions initiales, l’état convergera vers la référence plutôt que de tourner sans fin comme ce serait le cas avec une commande avec rétroaction pure.
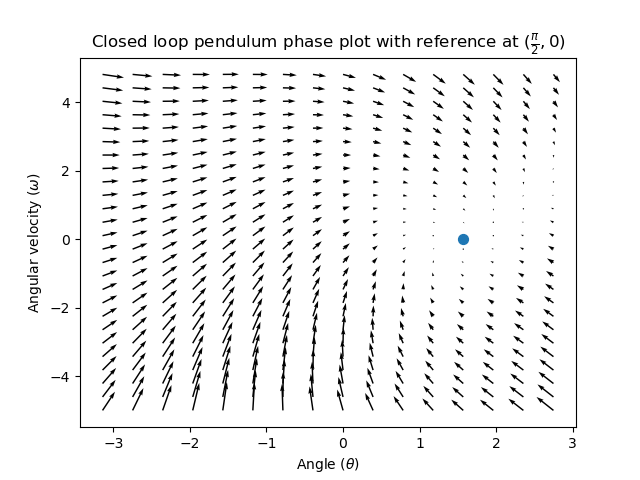
Mais comment choisir une matrice de gain K optimale pour notre système? Alors que nous pouvons choisir manuellement les gains et simuler la réponse du système ou l’ajuster sur le robot comme un contrôleur PID, la théorie de commande moderne a une meilleure réponse: le régulateur linéaire-quadratique (LQR).
Le régulateur linéaire-quadratique
Comme la commande basée sur un modèle signifie que nous pouvons prédire les états futurs d’un système étant données une condition initiale et des entrées de commande futures, nous pouvons choisir une matrice de gain math:mathbf {K} mathématiquement optimale. À cette fin, nous devons d’abord définir à quoi correspondrait une « bonne » ou « mauvaise » matrice \(\mathbf{K}\). Pour ce faire, nous additionnons dans le temps le carré de l’erreur et de l’entrée de commande, ceci nous donne un nombre représentant à quel point notre loi de contrôle sera « mauvaise ». Si nous minimisons cette somme, nous arrivons à la loi de commande optimale recherchée.
LQR: Définition
Linear-Quadratic Regulators work by finding a control law that minimizes the following cost function, which weights the sum of error and control effort over time, subject to the linear system dynamics \(\mathbf{x_{k+1} = Ax_k + Bu_k}\).
The control law that minimizes \(\mathbf{J}\) can be written as \(\mathbf{u = K(r_k - x_k)}\), where \(r_k - x_k\) is the error.
Note
Les matrices \(\mathbf{Q}\) et \(\mathbf{R}\) d’un modèle n’ont pas besoin de discrétisation, mais les matrices \(\mathbf{K}\) calculées pour les systèmes en temps continu et en temps discret seront différentes.
LQR: réglage
Tout comme les contrôleurs PID peuvent être réglés en ajustant leurs gains, nous voulons également changer la façon dont notre loi de commande équilibre notre erreur et notre entrée. Par exemple, un vaisseau spatial peut vouloir minimiser le carburant qu’il dépense pour atteindre une référence donnée, tandis qu’un bras robotique à grande vitesse peut avoir besoin de réagir rapidement aux perturbations.
Nous pouvons pondérer l’erreur et contrôler l’effort dans notre modèle LQR avec les matrices \(\mathbf{Q}\) et \(\mathbf{R}\). Dans notre fonction de coût (qui décrit la « mauvaise » performance de notre loi de commande), \(\mathbf{Q}\) et \(\mathbf{R}\) pondèrent notre erreur et les entrées de commande l’une par rapport à l’autre. Dans l’exemple de vaisseau spatial ci-dessus, nous pourrions utiliser une matrice \(\mathbf{Q}\) avec des valeurs relativement faibles pour montrer que nous ne voulons pas pénaliser fortement l’erreur, tandis que notre \(\mathbf{R}\) pourrait être élevée pour montrer que dépenser du carburant n’est pas souhaitable.
Avec WPILib, la classe LQR prend un vecteur d’excursions d’état maximum souhaitées et d’efforts de contrôle et les convertit en interne en matrices Q et R complètes avec la règle de Bryson. Nous utilisons souvent des minuscules \(\mathbf{q}\) et \(\mathbf{r}\) pour faire référence à ces vecteurs, et \(\mathbf{Q}\) et \(\mathbf{R}\) pour faire référence aux matrices.
Increasing the \(\mathbf{q}\) elements would make the LQR less heavily weight large errors, and the resulting control law will behave more conservatively. This has a similar effect to penalizing control effort more heavily by decreasing \(\mathbf{r}\)'s elements.
Similarly, decreasing the \(\mathbf{q}\) elements would make the LQR penalize large errors more heavily, and the resulting control law will behave more aggressively. This has a similar effect to penalizing control effort less heavily by increasing \(\mathbf{r}\) elements.
Par exemple, nous pourrions utiliser les Q et R suivants pour un système d’élévateur avec des états de position et de vitesse.
// Example system -- must be changed to match your robot.
LinearSystem<N2, N1, N1> elevatorSystem = LinearSystemId.identifyPositionSystem(5, 0.5);
LinearQuadraticRegulator<N2, N1, N1> controller = new LinearQuadraticRegulator(elevatorSystem,
// q's elements
VecBuilder.fill(0.02, 0.4),
// r's elements
VecBuilder.fill(12.0),
// our dt
0.020);
// Example system -- must be changed to match your robot.
LinearSystem<2, 1, 1> elevatorSystem = frc::LinearSystemId::IdentifyVelocitySystem(5, 0.5);
LinearQuadraticRegulator<2, 1> controller{
elevatorSystem,
// q's elements
{0.02, 0.4},
// r's elements
{12.0},
// our dt
0.020_s};
from wpimath.controller import LinearQuadraticRegulator_2_1
from wpimath.system.plant import LinearSystemId
# Example system -- must be changed to match your robot.
elevatorSystem = LinearSystemId.identifyPositionSystemMeters(5, 0.5)
controller = LinearQuadraticRegulator_2_1(
elevatorSystem,
# q's elements
(0.02, 0.4),
# r's elements
(12.0,),
# our dt
0.020,
)
LQR: exemple d’application
Let’s apply a Linear-Quadratic Regulator to a real-world example. Say we have a flywheel velocity system determined through system identification to have \(K_v = 1 \frac{\text{volts}}{\text{radian per second}}\) and \(K_a = 1.5 \frac{\text{volts}}{\text{radian per second squared}}\). Using the flywheel example above, we have the following linear system:
Nous choisissons arbitrairement une excursion d’état désirée (erreur maximale) de \(q = [0.1\ \text{rad/sec}]\), et un \(\mathbf{r}\) de \([12\ \text{volts}]\). Après discrétisation avec un pas de temps de 20ms, on trouve un gain de \(\mathbf{K} = ~81\). Ce gain K agit comme la composante proportionnelle d’une boucle PID sur la vitesse du volant d’inertie.
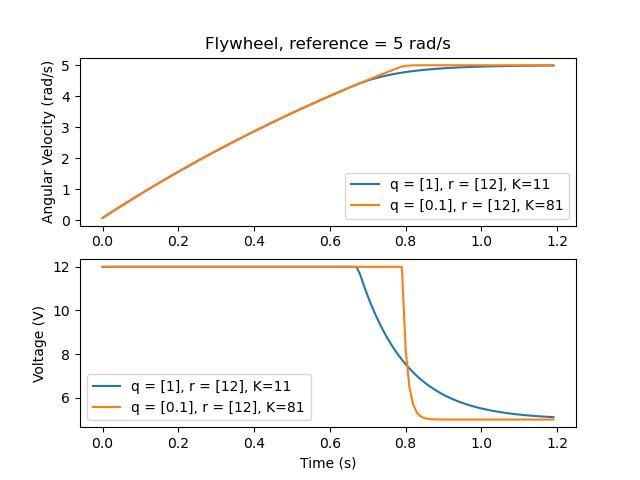
Let’s adjust \(\mathbf{q}\) and \(\mathbf{r}\). We know that increasing the q elements or decreasing the \(\mathbf{r}\) elements we use to create \(\mathbf{Q}\) and \(\mathbf{R}\) would make our controller more heavily penalize control effort, analogous to trying to driving a car more conservatively to improve fuel economy. In fact, if we increase our error tolerance q from 0.1 to 1.0, our gain matrix \(\mathbf{K}\) drops from ~81 to ~11. Similarly, decreasing our maximum voltage \(r\) from 12.0 to 1.2 decreases \(\mathbf{K}\).
Le graphique suivant montre la vitesse angulaire du volant d’inertie et la tension appliquée au fil du temps avec deux gains. Nous pouvons voir comment un gain plus élevé permettra au système d’atteindre la référence plus rapidement (à t = 0.8 seconde), tout en maintenant notre moteur saturé à 12V plus longtemps. C’est exactement la même chose que d’augmenter le gain P d’un régulateur PID d’un facteur ~ 8x.
LQR et compensation de latence de mesure
Souvent, nos capteurs ont un retard associé à leurs mesures. Par exemple, le contrôleur de moteur SPARK MAX sur CAN peut avoir jusqu’à 30 ms de retard associé aux mesures de vitesse.
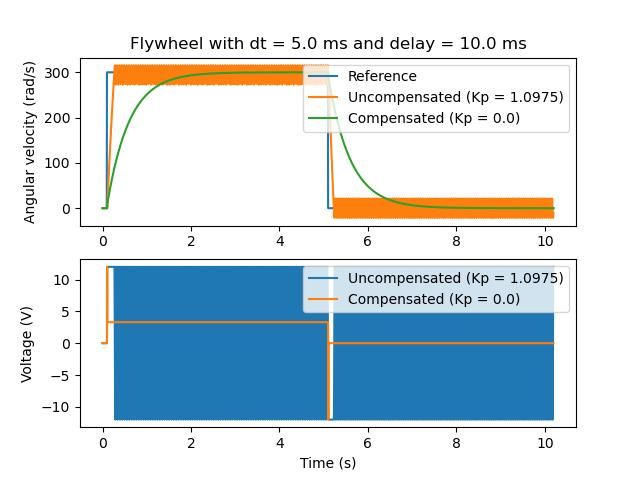
Ce décalage signifie que notre contrôleur de rétroaction générera des commandes de tension basées sur des estimations d’état du passé. Cela a souvent pour effet d’introduire de l’instabilité et des oscillations dans notre système, comme le montre le graphique ci-dessous.
Cependant, nous pouvons modéliser notre contrôleur pour contrôler où le state du système est retardé dans le futur. Cela réduira la matrice gain du LQR \(\mathbf{K}\), échangeant les performances du contrôleur contre la stabilité. La formule ci-dessous, qui ajuste la matrice gain pour tenir compte du retard, est également utilisée dans l’identification du système.
Multiplier \(\mathbf{K}\) par \(\mathbf{A} - \mathbf{BK}\) avance essentiellement les gains d’un pas de temps. Dans ce cas, on multiplie par \(\left(\mathbf{A} - \mathbf{BK}\right)^{\text{delay} / dt}\) pour avancer les gains par le retard de la mesure.
Note
Cela peut avoir pour effet de réduire \(\mathbf{K}\) à zéro, désactivant ainsi la commande de rétroaction.
Note
Le contrôleur de moteur SPARK MAX utilise un filtre à réponse impulsionnelle finie ou RIF à 40 prises avec un retard de 19.5 ms, et les trames d’état sont envoyées par défaut tous les 20ms.
Le code ci-dessous montre comment régler le gain K du contrôleur LQR pour les délais d’entrée du capteur:
// Adjust our LQR's controller for 25 ms of sensor input delay. We
// provide the linear system, discretization timestep, and the sensor
// input delay as arguments.
controller.latencyCompensate(elevatorSystem, 0.02, 0.025);
// Adjust our LQR's controller for 25 ms of sensor input delay. We
// provide the linear system, discretization timestep, and the sensor
// input delay as arguments.
controller.LatencyCompensate(elevatorSystem, 20_ms, 25_ms);
# Adjust our LQR's controller for 25 ms of sensor input delay. We
# provide the linear system, discretization timestep, and the sensor
# input delay as arguments.
controller.latencyCompensate(elevatorSystem, 0.020, 0.025)
Linéarisation
La linéarisation est un outil utilisé pour approximer les fonctions non linéaires et les systèmes d’espace d’états en faisant usage de systèmes linéaires. Dans l’espace bidimensionnel, les fonctions linéaires sont des lignes droites tandis que les fonctions non linéaires sont courbes. Un exemple courant de fonction non linéaire et de son approximation linéaire correspondante est: \(y=\sin{x}\). Cette fonction peut être approximée par \(y=x\) près de zéro. Cette approximation est précise lorsqu’elle est proche de \(x=0\), mais perd de la précision lorsque nous nous éloignons du point de linéarisation. Par exemple, l’approximation \(\sin{x} \approx x\) est précise à 0.02 près de 0.5 radians de \(y = 0\), mais perd rapidement sa précision au-delà. Dans l’image suivante, nous voyons \(y =\sin{x}\), \(y=x\) et la différence entre l’approximation et la vraie valeur de \(\sin{x}\) à \(x\).
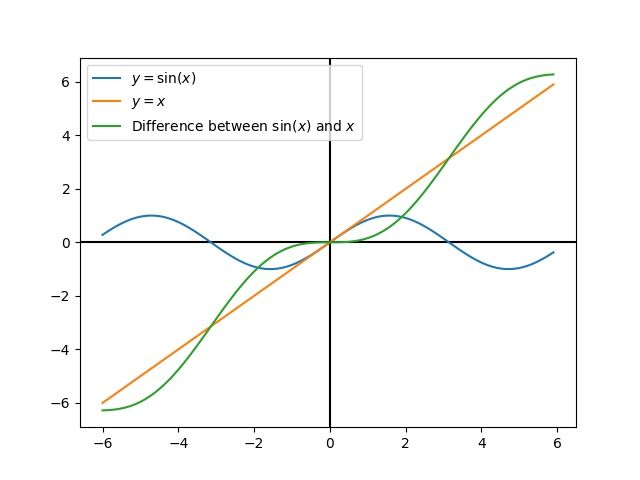
Nous pouvons également linéariser des systèmes d’espace d’états en faisant appel à une dynamique non-linéaire. Pour ce faire, choisissons un point \(\mathbf{x}\) dans l’espace d’états et en utilisons-le comme entrée de nos fonctions non linéaires. Comme dans l’exemple ci-dessus, cela fonctionne bien pour les états proches du point sur lequel le système a été linéarisé, mais peut rapidement diverger davantage de cet état.