Les notions fondamentales d’un système de contrôle
Note
This article includes sections of Controls Engineering in FRC by Tyler Veness with permission.
The Need for Control Systems
Les systèmes de contrôle sont présents tout autour de nous et nous interagissons quotidiennement avec eux. Une petite liste de ceux que vous avez peut-être vus comprend: des radiateurs et des climatiseurs avec thermostats, un régulateur de vitesse pour une voiture, ou son système de freinage antiblocage (ABS), et la modulation de la vitesse du ventilateur sur les ordinateurs portables modernes. Les systèmes de contrôle surveillent ou contrôlent le comportement de systèmes comme ceux-ci et peuvent être activées par des opérateurs humains (contrôle manuel), ou uniquement par des machines (contrôle automatique).
All of these examples have a mechanism which does useful work, but cannot be directly commanded to the state that is desired.
For example, an air conditioner’s fans and compressor have no mechanical or electrical input where the user specifies a temperature. Rather, some additional mechanism must compare the current air temperature to some setpoint, and choose how to cycle the compressor and fans on and off to achieve that temperature.
Similarly, an automobile’s engine and transmission have no mechanical lever which directly sets a particular speed. Rather, some additional mechanism must measure the current speed of the vehicle, and adjust the transmission gear and fuel injected into the cylinders to achieve the desired vehicle speed.
Controls Engineering is the study of how to design those additional mechanisms to bridge the gap from what the user wants a mechanism to do, to how the mechanism is actually manipulated.
Comment pouvons-nous prouver que les contrôleurs en boucle fermée sur une voiture autonome, par exemple, se comporteront en toute sécurité et répondront aux spécifications de performance souhaitées en présence d’incertitude? La théorie du contrôle est une application de l’algèbre et de la géométrie utilisée pour analyser et prédire le comportement des systèmes, les faire réagir comme nous le voulons et les rendre robustes aux perturbations et à l’incertitude.
L’ingénierie des contrôles est, en termes simples, le processus d’ingénierie appliqué à la théorie du contrôle. En tant que tel, c’est plus que des mathématiques appliquées. Alors que la théorie du contrôle a de belles mathématiques derrière elle, l’ingénierie des contrôles est une discipline d’ingénierie comme les autres qui est pleine de compromis. Les solutions que la théorie du contrôle donne doivent toujours être vérifiées et conformes à nos spécifications de performance. Nous n’avons pas besoin d’être parfaits; nous devons juste être assez bons pour répondre à nos spécifications.
Nomenclature
La plupart des ressources pour les sujets d’ingénierie avancée supposent un niveau de connaissances bien supérieur à ce qui est nécessaire. Une partie du problème est l’utilisation du jargon (langage technique). Bien que ce langage communique efficacement les idées à ceux qui travaillent dans ce domaine, les initiés qui ne le connaissent pas sont perdues.
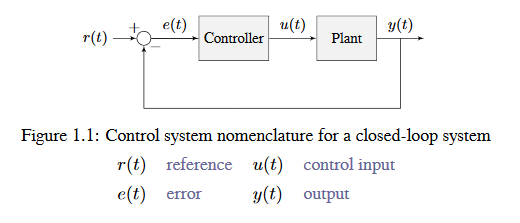
Le système ou la série de senseurs et actuateurs contrôlés par un système de commande est appelé Usine, (Plant, en anglais). Un contrôleur est utilisé pour amener l’état actuel de l’Usine à un état souhaité (la référence). Les contrôleurs qui n’incluent pas d’informations mesurées à partir de la sortie de l’Usine sont appelés contrôleurs en boucle ouverte.
Les contrôleurs qui intègrent les informations renvoyées par la sortie de l’Usine sont appelés contrôleurs en boucle fermée ou contrôleurs de rétroaction.
Note
L’entrée et la sortie d’un système sont définies du point de vue de l’installation. Le contrôleur de rétroaction négative illustré conduit à zéro la différence entre la référence et la sortie, également connue sous le nom d’erreur.
Qu’est-ce que le gain?
Gain est une valeur proportionnelle qui montre la relation entre l’amplitude d’un signal d’entrée et l’amplitude d’un signal de sortie à l’état stationnaire (Steady-state). De nombreux systèmes contiennent une méthode par laquelle le gain peut être modifié, fournissant plus ou moins de «puissance» au système.
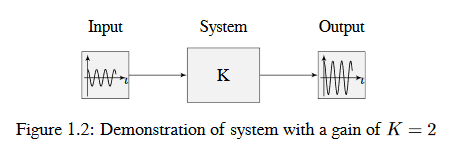
La figure ci-dessous montre un système avec une entrée et une sortie hypothétiques. Étant donné que la sortie est deux fois l’amplitude de l’entrée, le système a un gain de deux.
What is a Model?
A model of your mechanism is a mathematical description of its behavior. Specifically, this mathematical description must define the mechanism’s inputs and outputs, and how the output values change over time as a function of its input values.
The mathematical description is often just simple algebra equations. It can also include some linear algebra, matrices, and differential equations. WPILib provides a number of classes to help simplify the more complex math.
Classical Mechanics defines many of the equations used to build up models of system behavior. Many of the values inside those equations can be determined by doing experiments on the mechanism.
Schémas fonctionnels
Lors de la conception ou de l’analyse d’un système de contrôle, il est utile de le modéliser graphiquement. Des schémas fonctionnels sont utilisés à cet effet. Ils peuvent être manipulés et simplifiés systématiquement.
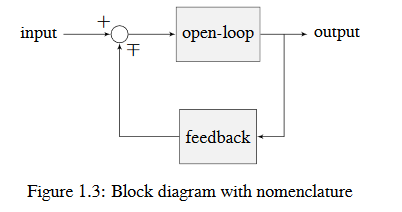
Le gain en boucle ouverte est le gain total du nœud de somme à l’entrée (le cercle) vers la branche de sortie. ce serait le gain du système si la boucle de rétroaction était déconnectée. Le gain de rétroaction est le gain total de la sortie vers le nœud de somme d’entrée. La sortie d’un nœud de somme est calculée en additionnant toutes ses entrées.
La figure ci-dessous est un schéma illustrant une configuration de rétroaction, avec la bonne nomenclature.
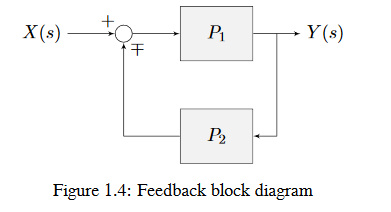
\(\mp\) signifie « moins ou plus » où un signe moins représente une rétroaction négative.
A Note on Dimensionality
For the purposes of the introductory section, all systems and controllers (except feedforward controllers) are assumed to be « single-in, single-out » (SISO) - this means they only map single values to single values. For example, a DC motor is considered to take an input of a single scalar value (voltage) and yield an output of only a single scalar value in return (either position or velocity). This forces us to consider position controllers and velocity controllers as separate entities - this is sometimes source of confusion in situations when we want to control both (such as when following a motion profiles). Limiting ourselves to SISO systems also means that we are unable to analyze more-complex « multiple-in, multiple-out » (MIMO) systems like drivetrains that cannot be represented with a single state (there are at least two independent sets of wheels in a drive).
Nonetheless, we restrict ourselves to SISO systems here to be able to present the following tutorials in terms of the PID Controller formalism, which is commonly featured in introductory course material and has extensive documentation and many available implementations.
The state-space formalism is an alternate way to conceptualize these systems which allows us to easily capture interactions between different quantities (as well as simultaneously represent multiple aspects of the same quantity, such as position and velocity of a motor). It does this, roughly, by replacing the single-dimensional scalars (e.g. the gain, input, and output) with multi-dimensional vectors. In the state-space formalism, the equivalent of a « PID » controller is a vector-proportional controller on a single vector-valued mechanism state, with a single gain vector (instead of three different gain scalars).
If you remember that a state-space controller is really just a PID controller written with dense notation, many of the principles covered in this set of introductory articles will transfer seamlessly to the case of state-space control.