Description de l’espace-état d’un controleur
Note
Avant de poursuivre la lecture de ce didacticiel, il est recommandé aux lecteurs d’avoir pris connaissance du document Introduction au Contrôle de l’Espace-État.
L’objectif de ce didacticiel est de fournir des instructions de « bout à bout » sur la mise en œuvre dans l’espace d’état d’un contrôleur pour un volant d’inertie. En parcourant ce didacticiel, les lecteurs apprendront à:
Create an accurate state-space model of a flywheel using system identification or CAD software.
Implémenter un filtre de Kalman pour filtrer les mesures de vitesse de l’encodeur sans décalage.
implémenter une commande LQR de rétroaction qui, lorsqu’elle est combinée avec le modèle de commande prédictive, générera les tensions d’entrée afin de conduire le volant d’inertie à la référence.
Ce tutoriel se veut être simple pour faciliter la tâche aux équipes n’ayant pas beaucoup d’expertise en programmation. Bien que la bibliothèque WPILib offre une flexibilité significative dans la manière dont ses fonctionnalités de contrôle dans l’espace d’état sont implémentées, parcourir attentivement l’implémentation décrite dans ce didacticiel devrait fournir aux équipes une structure de base qui peut être réutilisée pour une variété de systèmes espace-état.
The full example is available in the state-space flywheel (Java/C++/Python) and state-space flywheel system identification (Java/C++/Python) example projects.
Pourquoi utiliser le contrôle espace-état ?
Étant donné que la commande de l’espace-état se concentre sur la création d’un modèle précis de notre système, nous pouvons adéquatement prédire comment notre modèle va répondre aux entrées des commandes. Cela nous permet de simuler nos mécanismes sans accès à un robot physique, ainsi que de choisir facilement les gains que nous savons parfaitement fonctionnels. Avoir un modèle nous permet également de créer des filtres sans retard, comme les filtres de Kalman, pour filtrer de manière optimale les signaux obtenus à partir des capteurs.
Modélisation de notre volant d’inertie
Rappelons que les systèmes continus espace-état sont modélisés à l’aide du système d’équations suivant:
Where x-dot is the rate of change of the system’s state, \(\mathbf{x}\) is the system’s current state, \(\mathbf{u}\) is the input to the system, and \(\mathbf{y}\) is the system’s output.
Utilisons ce système d’équations pour modéliser notre volant d’inertie de deux manières différentes. Nous allons d’abord le modéliser en utilisant identification du système à l’aide de la suite d’outils SysId, puis le modéliser en fonction du moment d’inertie du moteur et du volant.
The first step of building up our state-space system is picking our system’s states. We can pick anything we want as a state – we could pick completely unrelated states if we wanted – but it helps to pick states that are important. We can include hidden states in our state (such as elevator velocity if we were only able to measure its position) and let our Kalman Filter estimate their values. Remember that the states we choose will be driven towards their respective references by the feedback controller (typically the Linear-Quadratic Regulator since it’s optimal).
For our flywheel, we care only about one state: its velocity. While we could chose to also model its acceleration, the inclusion of this state isn’t necessary for our system.
Ensuite, nous identifions les entrées dans notre système. Les entréss peuvent être considérées comme des paramètres que nous pouvons mettre « dans » notre système pour en changer l’état. Dans le cas du volant d’inertie (et de nombreux autres mécanismes à simple articulation en FRC®), nous n’avons qu’une seule entrée : la tension appliquée sur le moteur. En choisissant la tension comme entrée (plutôt qu’un paramètre comme le cycle de travail du moteur), nous pouvons compenser la réduction de la tension de la batterie à mesure que la charge de la batterie augmente.
Un système espace-état en temps continu écrit x-point, ou le taux de variation instantané de l’état du système, comme proportionnel à l’état actuel et ses entrées. Puisque notre état est la vitesse angulaire, \(\mathbf{\dot{x}}\) sera l’accélération angulaire du volant d’inertie.
Ensuite, nous allons modéliser notre volant d’inertie comme un système espace-état en temps continu. Le LinearSystem de WPILib convertira ce système en temps discret selon un mécanisme interne. Relisez la notation espace-état pour en savoir d’avantage sur les systèmes en temps continu et en temps discret.
Modélisation par identification du système
To rewrite this in state-space notation using system identification, we recall from the flywheel state-space notation example, where we rewrote the following equation in terms of \(\mathbf{a}\).
Où \(\mathbf{v}\) est la vitesse du volant d’inertie, \(\mathbf{a}\) et \(\mathbf{\dot{v}}\) sont l’accélération de la roue d’inertie, et \(V\) est la tension. En reformulant ce qui précède selon la représentation conventionnelle \(\mathbf{x}\) pour le vecteur d’état et \(\mathbf{u}\) pour le vecteur d’entrée, nous trouvons:
La deuxième partie de la notation espace-état relie les termes actuels du système état et entrées à la sortie. Dans le cas d’un volant d’inertie, notre vecteur de sortie \(\mathbf{y}\) (ou toute autre grandeur que nos capteurs peuvent mesurer) est la vitesse de notre volant d’inertie, qui se trouve également être un élément de notre vecteur d’état \(\mathbf{x}\). Par conséquent, notre matrice de sortie est \(\mathbf{C} = \begin{bmatrix}1 \end{bmatrix}\), et notre matrice du système de la traversée est \(\mathbf{D} = \begin{bmatrix}0 \end{bmatrix}\). En reformulant ce qui précède selon la notation espace-état en temps continu conduit au résultat suivant.
La classe LinearSystem contient des méthodes permettant de créer facilement des systèmes espace-état identifiés à l’aide de la méthode d’identification de système. Cet exemple montre un modèle volant d’inertie avec un kV de 0.023 et un kA de 0.001 :
33 // Volts per (radian per second)
34 private static final double kFlywheelKv = 0.023;
35
36 // Volts per (radian per second squared)
37 private static final double kFlywheelKa = 0.001;
38
39 // The plant holds a state-space model of our flywheel. This system has the following properties:
40 //
41 // States: [velocity], in radians per second.
42 // Inputs (what we can "put in"): [voltage], in volts.
43 // Outputs (what we can measure): [velocity], in radians per second.
44 //
45 // The Kv and Ka constants are found using the FRC Characterization toolsuite.
46 private final LinearSystem<N1, N1, N1> m_flywheelPlant =
47 LinearSystemId.identifyVelocitySystem(kFlywheelKv, kFlywheelKa);
17#include <frc/system/plant/LinearSystemId.h>
30 // Volts per (radian per second)
31 static constexpr auto kFlywheelKv = 0.023_V / 1_rad_per_s;
32
33 // Volts per (radian per second squared)
34 static constexpr auto kFlywheelKa = 0.001_V / 1_rad_per_s_sq;
35
36 // The plant holds a state-space model of our flywheel. This system has the
37 // following properties:
38 //
39 // States: [velocity], in radians per second.
40 // Inputs (what we can "put in"): [voltage], in volts.
41 // Outputs (what we can measure): [velocity], in radians per second.
42 //
43 // The Kv and Ka constants are found using the FRC Characterization toolsuite.
44 frc::LinearSystem<1, 1, 1> m_flywheelPlant =
45 frc::LinearSystemId::IdentifyVelocitySystem<units::radian>(kFlywheelKv,
46 kFlywheelKa);
23# Volts per (radian per second)
24kFlywheelKv = 0.023
25
26# Volts per (radian per second squared)
27kFlywheelKa = 0.001
37 # The plant holds a state-space model of our flywheel. This system has the following properties:
38 #
39 # States: [velocity], in radians per second.
40 # Inputs (what we can "put in"): [voltage], in volts.
41 # Outputs (what we can measure): [velocity], in radians per second.
42 #
43 # The Kv and Ka constants are found using the FRC Characterization toolsuite.
44 self.flywheelPlant = (
45 wpimath.system.plant.LinearSystemId.identifyVelocitySystemRadians(
46 kFlywheelKv, kFlywheelKa
47 )
48 )
Modélisation à l’aide du moment d’inertie du volant d’inertie et de l’engrenage.
A flywheel can also be modeled without access to a physical robot, using information about the motors, gearing and flywheel’s moment of inertia. A full derivation of this model is presented in Section 12.3 of Controls Engineering in FRC.
The LinearSystem class contains methods to easily create a model of a flywheel from the flywheel’s motors, gearing and moment of inertia. The moment of inertia can be calculated using CAD software or using physics. The examples used here are detailed in the flywheel example project (Java/C++/Python).
Note
Pour les classes espace-état de la WPILib, l’engrenage est modélisé par une fonction de sortie sur entrée – c’est-à-dire que si le volant d’inertie tourne plus lentement que les moteurs, ce nombre devrait être supérieur à un.
Note
La classe C++ LinearSystem utilise librairie d’unités C++ pour prévenir les mélanges des unités et se conformer à l’analyse dimensionnelle.
33 private static final double kFlywheelMomentOfInertia = 0.00032; // kg * m^2
34
35 // Reduction between motors and encoder, as output over input. If the flywheel spins slower than
36 // the motors, this number should be greater than one.
37 private static final double kFlywheelGearing = 1.0;
38
39 // The plant holds a state-space model of our flywheel. This system has the following properties:
40 //
41 // States: [velocity], in radians per second.
42 // Inputs (what we can "put in"): [voltage], in volts.
43 // Outputs (what we can measure): [velocity], in radians per second.
44 private final LinearSystem<N1, N1, N1> m_flywheelPlant =
45 LinearSystemId.createFlywheelSystem(
46 DCMotor.getNEO(2), kFlywheelMomentOfInertia, kFlywheelGearing);
17#include <frc/system/plant/LinearSystemId.h>
31#include <frc/system/plant/LinearSystemId.h>
32 static constexpr units::kilogram_square_meter_t kFlywheelMomentOfInertia =
33 0.00032_kg_sq_m;
34
35 // Reduction between motors and encoder, as output over input. If the flywheel
36 // spins slower than the motors, this number should be greater than one.
37 static constexpr double kFlywheelGearing = 1.0;
38
39 // The plant holds a state-space model of our flywheel. This system has the
40 // following properties:
41 //
42 // States: [velocity], in radians per second.
43 // Inputs (what we can "put in"): [voltage], in volts.
44 // Outputs (what we can measure): [velocity], in radians per second.
45 frc::LinearSystem<1, 1, 1> m_flywheelPlant =
46 frc::LinearSystemId::FlywheelSystem(
47 frc::DCMotor::NEO(2), kFlywheelMomentOfInertia, kFlywheelGearing);
21kFlywheelMomentOfInertia = 0.00032 # kg/m^2
22
23# Reduction between motors and encoder, as output over input. If the flywheel spins slower than
24# the motors, this number should be greater than one.
25kFlywheelGearing = 1
37 # The plant holds a state-space model of our flywheel. This system has the following properties:
38 #
39 # States: [velocity], in radians per second.
40 # Inputs (what we can "put in"): [voltage], in volts.
41 # Outputs (what we can measure): [velocity], in radians per second.
42 self.flywheelPlant = wpimath.system.plant.LinearSystemId.flywheelSystem(
43 wpimath.system.plant.DCMotor.NEO(2),
44 kFlywheelMomentOfInertia,
45 kFlywheelGearing,
46 )
Filtres de Kalman : Observation de l’état du volant d’inertie
Les filtres de Kalman sont utilisés pour filtrer nos mesures de vitesse à l’aide de notre modèle espace-état pour générer une estimation de l’état \(\mathbf{\hat{x}}\). Comme notre modèle de volant est linéaire, nous pouvons utiliser un filtre de Kalman pour estimer la vitesse du volant. Le filtre de Kalman fournie par la WPILib prend un système linéaire ou LinearSystem (que nous avons trouvé ci-dessus), ainsi que des écarts-types des mesures du modèle et des capteurs. Nous pouvons ajuster le « lissage » de notre de l’état estimé en ajustant ces poids. Les déviations standard plus importants de l’état feront en sorte que le filtre « se conforme moins » à notre estimation de l’état et favorisera plus fortement les nouvelles mesures, tandis que des valeurs plus grandes de déviations standard auront un effet contraire.
Dans le cas d’un volant d’inertie, nous commençons par un écart type d’état de 3 rad/s et un écart type de mesure de 0.01 rad/s. Le choix de ces valeurs est à la discrétion de l’utilisateur - ces poids ont produit un filtre qui était tolérant à certains bruits, mais dont l’estimation de l’état a rapidement réagi aux perturbations externes pour un volant d’inertie - et doivent être réglés pour créer un filtre qui soit conforme à votre volant spécifique. Les tracés des états, des mesures, des entrées, des références et des sorties au fil du temps sont un excellent moyen visuel de régler les filtres de Kalman.
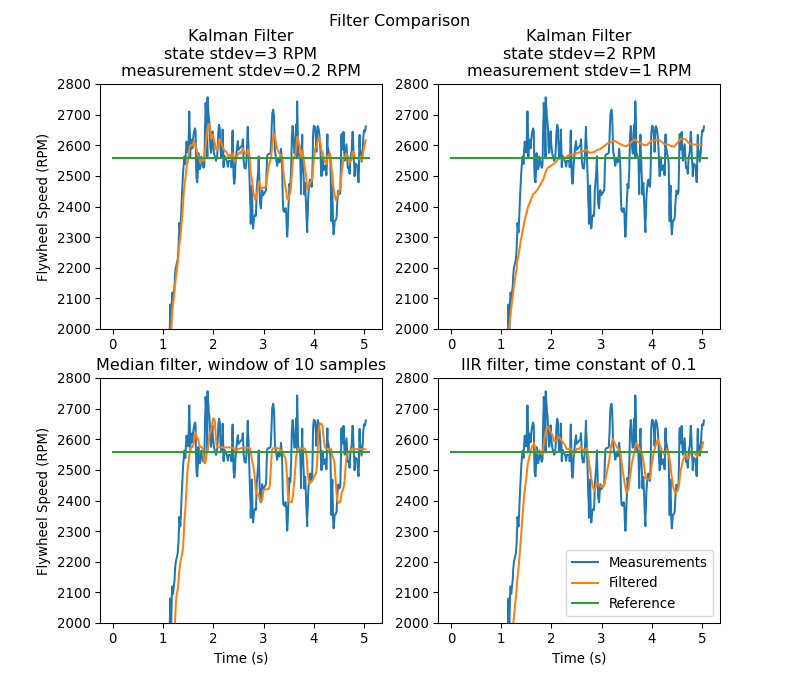
Le graphique ci-dessus montre deux filtres de Kalman réglés différemment, ainsi qu’un filtre IIR simple-pôle et un Filtre médian. Ces données ont été recueillies avec un tireur sur ~5 secondes, et quatre balles ont été lancées à travers le tireur (comme on le voit dans les quatre creux de vitesse). Bien qu’il n’y ait pas de règles strictes sur le choix du bon état et des écarts-types des mesures, ils devraient en général être réglés pour se rapprocher suffisamment du modèle pour éliminer le bruit tout en réagissant rapidement aux perturbations externes.
Comme le contrôleur de rétroaction calcule l’erreur à l’aide du paramètre x-chapeau estimé par le filtre de Kalman, le contrôleur ne réagira aux perturbations qu’aussi rapidement que l’estimation d’état du filtre change. Dans le graphique ci-dessus, la courbe située en haut et à gauche (avec un écart type d’état de 3.0 et un écart type de mesure de 0.2) a produit un filtre qui réagit rapidement aux perturbations tout en rejetant le bruit, tandis que la courbe située en haut et à droite montre un filtre qui a été à peine affecté par les baisses de vitesse.
48 // The observer fuses our encoder data and voltage inputs to reject noise.
49 private final KalmanFilter<N1, N1, N1> m_observer =
50 new KalmanFilter<>(
51 Nat.N1(),
52 Nat.N1(),
53 m_flywheelPlant,
54 VecBuilder.fill(3.0), // How accurate we think our model is
55 VecBuilder.fill(0.01), // How accurate we think our encoder
56 // data is
57 0.020);
13#include <frc/estimator/KalmanFilter.h>
48 // The observer fuses our encoder data and voltage inputs to reject noise.
49 frc::KalmanFilter<1, 1, 1> m_observer{
50 m_flywheelPlant,
51 {3.0}, // How accurate we think our model is
52 {0.01}, // How accurate we think our encoder data is
53 20_ms};
48 # The observer fuses our encoder data and voltage inputs to reject noise.
49 self.observer = wpimath.estimator.KalmanFilter_1_1_1(
50 self.flywheelPlant,
51 [3], # How accurate we think our model is
52 [0.01], # How accurate we think our encoder data is
53 0.020,
54 )
Étant donné que les filtres de Kalman utilisent notre modèle espace-état dans L’étape de prédiction, il est important que notre modèle soit aussi précis que possible. Une façon de vérifier cela est d’enregistrer la tension d’entrée et la vitesse d’entrée d’un volant d’inertie au fil du temps, et de rejouer ces données en appelant uniquement predict sur le filtre de Kalman. Ensuite, les gains kV et kA (ou moment d’inertie et autres constantes) peuvent être ajustés jusqu’à ce que le modèle corresponde étroitement aux données enregistrées.
Régulateurs linéaires-quadratiques et commande prédictive inverse de procédé
Le régulateur linéaire-quadratique trouve un contrôleur de rétroaction pour amener notre système volant d’inertie à sa référence. Parce que notre volant n’a qu’un seul état, la loi de commande choisie par notre LQR sera sous la forme \(\mathbf{u = K (r - x)}\) où \(\mathbf{K}\) est une matrice 1x1; en d’autres termes, la loi de commande choisie par notre LQR est simplement un contrôleur proportionnel, ou un contrôleur PID avec seulement un gain P. Ce gain est choisi par notre LQR en fonction de l’excursion d’état et des efforts de contrôle que nous lui transmettons. En savoir plus sur le réglage des contrôleurs LQR, consultez LQR application example.
Tout comme le SimpleMotorFeedforward peut être utilisé pour générer des tensions d’entrée de la commande prédictive étant donnés les constantes kS, kV, et kA, la classe Plant Inversion Feedforward génère feedforward les tensions d’entrée étant donné le système espace-état. Les commandes de tension générées par la classe LinearSystemLoop sont la somme des entrées des commandes prédictive et de rétroaction.
59 // A LQR uses feedback to create voltage commands.
60 private final LinearQuadraticRegulator<N1, N1, N1> m_controller =
61 new LinearQuadraticRegulator<>(
62 m_flywheelPlant,
63 VecBuilder.fill(8.0), // qelms. Velocity error tolerance, in radians per second. Decrease
64 // this to more heavily penalize state excursion, or make the controller behave more
65 // aggressively.
66 VecBuilder.fill(12.0), // relms. Control effort (voltage) tolerance. Decrease this to more
67 // heavily penalize control effort, or make the controller less aggressive. 12 is a good
68 // starting point because that is the (approximate) maximum voltage of a battery.
69 0.020); // Nominal time between loops. 0.020 for TimedRobot, but can be
70 // lower if using notifiers.
11#include <frc/controller/LinearQuadraticRegulator.h>
54 // A LQR uses feedback to create voltage commands.
55 frc::LinearQuadraticRegulator<1, 1> m_controller{
56 m_flywheelPlant,
57 // qelms. Velocity error tolerance, in radians per second. Decrease this
58 // to more heavily penalize state excursion, or make the controller behave
59 // more aggressively.
60 {8.0},
61 // relms. Control effort (voltage) tolerance. Decrease this to more
62 // heavily penalize control effort, or make the controller less
63 // aggressive. 12 is a good starting point because that is the
64 // (approximate) maximum voltage of a battery.
65 {12.0},
66 // Nominal time between loops. 20ms for TimedRobot, but can be lower if
67 // using notifiers.
68 20_ms};
69
70 // The state-space loop combines a controller, observer, feedforward and plant
71 // for easy control.
72 frc::LinearSystemLoop<1, 1, 1> m_loop{m_flywheelPlant, m_controller,
73 m_observer, 12_V, 20_ms};
56 # A LQR uses feedback to create voltage commands.
57 self.controller = wpimath.controller.LinearQuadraticRegulator_1_1(
58 self.flywheelPlant,
59 [8], # qelms. Velocity error tolerance, in radians per second. Decrease
60 # this to more heavily penalize state excursion, or make the controller behave more
61 # aggressively.
62 [12], # relms. Control effort (voltage) tolerance. Decrease this to more
63 # heavily penalize control effort, or make the controller less aggressive. 12 is a good
64 # starting point because that is the (approximate) maximum voltage of a battery.
65 0.020, # Nominal time between loops. 0.020 for TimedRobot, but can be lower if using notifiers.
66 )
En rassemblant le tout: LinearSystemLoop
LinearSystemLoop combine notre système, notre contrôleur et notre observateur que nous avons créés plus tôt. Le constructeur montré instancie également un PlantInversionFeedforward.
72 // The state-space loop combines a controller, observer, feedforward and plant for easy control.
73 private final LinearSystemLoop<N1, N1, N1> m_loop =
74 new LinearSystemLoop<>(m_flywheelPlant, m_controller, m_observer, 12.0, 0.020);
15#include <frc/system/LinearSystemLoop.h>
71 // The state-space loop combines a controller, observer, feedforward and plant
72 // for easy control.
73 frc::LinearSystemLoop<1, 1, 1> m_loop{m_flywheelPlant, m_controller,
74 m_observer, 12_V, 20_ms};
68 # The state-space loop combines a controller, observer, feedforward and plant for easy control.
69 self.loop = wpimath.system.LinearSystemLoop_1_1_1(
70 self.flywheelPlant, self.controller, self.observer, 12.0, 0.020
71 )
Une fois que nous avons obtenu notre LinearSystemLoop, la dernière chose à faire est de l’exécuter. Pour ce faire, nous mettrons périodiquement à jour notre filtre de Kalman avec nos nouvelles mesures de vitesse d’encodeur et lui appliquerons de nouvelles commandes de tension. Dans cette optique, nous avons d’abord défini la référence, puis corrigé avec la vitesse actuelle du volant d’inertie, prédit le filtre de Kalman dans le prochain pas de temps, et appliqué les entrées générées à l’aide de getU.
95 @Override
96 public void teleopPeriodic() {
97 // Sets the target speed of our flywheel. This is similar to setting the setpoint of a
98 // PID controller.
99 if (m_joystick.getTriggerPressed()) {
100 // We just pressed the trigger, so let's set our next reference
101 m_loop.setNextR(VecBuilder.fill(kSpinupRadPerSec));
102 } else if (m_joystick.getTriggerReleased()) {
103 // We just released the trigger, so let's spin down
104 m_loop.setNextR(VecBuilder.fill(0.0));
105 }
106
107 // Correct our Kalman filter's state vector estimate with encoder data.
108 m_loop.correct(VecBuilder.fill(m_encoder.getRate()));
109
110 // Update our LQR to generate new voltage commands and use the voltages to predict the next
111 // state with out Kalman filter.
112 m_loop.predict(0.020);
113
114 // Send the new calculated voltage to the motors.
115 // voltage = duty cycle * battery voltage, so
116 // duty cycle = voltage / battery voltage
117 double nextVoltage = m_loop.getU(0);
118 m_motor.setVoltage(nextVoltage);
119 }
120}
5#include <numbers>
6
7#include <frc/DriverStation.h>
8#include <frc/Encoder.h>
9#include <frc/TimedRobot.h>
10#include <frc/XboxController.h>
11#include <frc/controller/LinearQuadraticRegulator.h>
12#include <frc/drive/DifferentialDrive.h>
13#include <frc/estimator/KalmanFilter.h>
14#include <frc/motorcontrol/PWMSparkMax.h>
15#include <frc/system/LinearSystemLoop.h>
16#include <frc/system/plant/DCMotor.h>
17#include <frc/system/plant/LinearSystemId.h>
92 void TeleopPeriodic() override {
93 // Sets the target speed of our flywheel. This is similar to setting the
94 // setpoint of a PID controller.
95 if (m_joystick.GetRightBumper()) {
96 // We pressed the bumper, so let's set our next reference
97 m_loop.SetNextR(frc::Vectord<1>{kSpinup.value()});
98 } else {
99 // We released the bumper, so let's spin down
100 m_loop.SetNextR(frc::Vectord<1>{0.0});
101 }
102
103 // Correct our Kalman filter's state vector estimate with encoder data.
104 m_loop.Correct(frc::Vectord<1>{m_encoder.GetRate()});
105
106 // Update our LQR to generate new voltage commands and use the voltages to
107 // predict the next state with out Kalman filter.
108 m_loop.Predict(20_ms);
109
110 // Send the new calculated voltage to the motors.
111 // voltage = duty cycle * battery voltage, so
112 // duty cycle = voltage / battery voltage
113 m_motor.SetVoltage(units::volt_t{m_loop.U(0)});
114 }
87 def teleopPeriodic(self) -> None:
88 # Sets the target speed of our flywheel. This is similar to setting the setpoint of a
89 # PID controller.
90 if self.joystick.getTriggerPressed():
91 # We just pressed the trigger, so let's set our next reference
92 self.loop.setNextR([kSpinUpRadPerSec])
93
94 elif self.joystick.getTriggerReleased():
95 # We just released the trigger, so let's spin down
96 self.loop.setNextR([0.0])
97
98 # Correct our Kalman filter's state vector estimate with encoder data.
99 self.loop.correct([self.encoder.getRate()])
100
101 # Update our LQR to generate new voltage commands and use the voltages to predict the next
102 # state with out Kalman filter.
103 self.loop.predict(0.020)
104
105 # Send the new calculated voltage to the motors.
106 # voltage = duty cycle * battery voltage, so
107 # duty cycle = voltage / battery voltage
108 nextVoltage = self.loop.U()
109 self.motor.setVoltage(nextVoltage)
Angle Wrap with LQR
Mechanisms with a continuous angle can have that angle wrapped by calling the code below instead of lqr.Calculate(x, r).
var error = lqr.getR().minus(x);
error.set(0, 0, MathUtil.angleModulus(error.get(0, 0)));
var u = lqr.getK().times(error);
Eigen::Vector<double, 2> error = lqr.R() - x;
error(0) = frc::AngleModulus(units::radian_t{error(0)}).value();
Eigen::Vector<double, 2> u = lqr.K() * error;
error = lqr.R() - x
error[0] = wpimath.angleModulus(error[0])
u = lqr.K() * error