Introducción al Control del Estado-Espacio
Nota
Este artículo es de Ingeniería de Controles en FRC por Tyler Veness con permiso.
De PID a Control Basado en Modelo
Al ajustar los controladores PID, nos centramos en jugar con los parámetros del controlador relacionados con el presente, el pasado y el futuro error (términos P, I y D) en lugar de los estados subyacentes del sistema. Si bien este enfoque funciona en muchas situaciones, es una visión incompleta del mundo.
El control basado en modelos se enfoca en desarrollar un modelo preciso de el system (mecanismo) que estamos tratando de controlar. Estos modelos ayudan a informar gains tomadas de controladores basados en respuestas físicas del sistema, en vez de un arbitrario gain proporcional derivado mediante pruebas. Esto nos permite no solo predecir a futuro como reaccionará el sistema, y también probará nuestros controladores sin un robot que esté físicamente y ahorrar tiempo depurando errores simples.
Nota
State-space control makes extensive use of linear algebra. More on linear algebra in modern control theory, including an introduction to linear algebra and resources, can be found in Chapter 5 of Controls Engineering in FRC.
If you’ve used WPILib’s feedforward classes for SimpleMotorFeedforward or its sister classes, or used SysId to pick PID gains for you, you’re already familiar with model-based control! The kv and ka gains can be used to describe how a motor (or arm, or drivetrain) will react to voltage. We can put these constants into standard state-space notation using WPILib’s LinearSystem, something we will do in a later article.
Vocabulario
Para el vocabulario de fondo que se utilizará a lo largo de este artículo, consulte el Glosario.
Introducción a Algebra Lineal
Para una introducción corta e intuitiva a los conceptos básicos de Álgebra Lineal, recomendamos los capítulos 1 al 4 de Series 3Blue1Brown Esencia del algebra lineal (Vectores, ¿qué son esos?, Combinaciones lineales, lapso, y vectores base, Transformaciones lineales y matrices, y Multiplicación de matrices como composición).
¿Qué es Estado-Espacio?
Recall that 2D space has two axes: x and y. We represent locations within this space as a pair of numbers packaged in a vector, and each coordinate is a measure of how far to move along the corresponding axis. State-space is a Cartesian coordinate system with an axis for each state variable, and we represent locations within it the same way we do for 2D space: with a list of numbers in a vector. Each element in the vector corresponds to a state of the system. This example shows two example state vectors in the state-space of an elevator model with the states \([\text{position}, \text{velocity}]\):
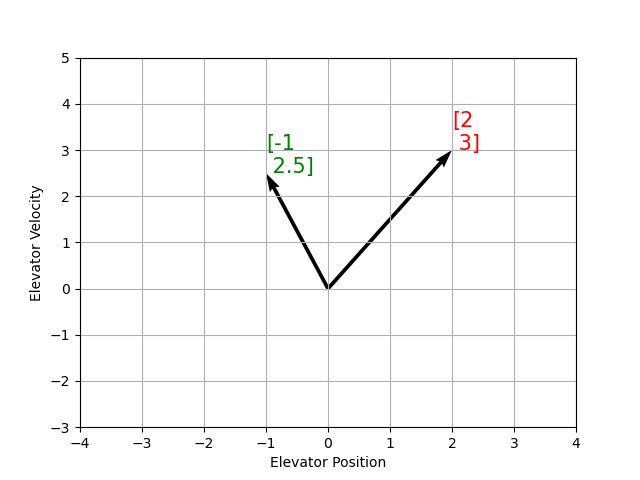
En ésta imagen, los vectores representando estados en estado-espacio son flechas. Desde ahora en éstos vectores serán representados simplemente por un punto en la punta del vector, pero recuerde que el resto del vector seguirá ahi.
Añadiendo al estado, entradas y salidas son representados como vectores. Dado que el mapeo de los estados actuales y las entradas al cambio de estado es un sistema de ecuaciones, es natural escribirlo en forma de matriz. Esta ecuación matricial se puede escribir en notación de estado-espacio.
¿Qué es la Notación de Estado-Espacio?
La notación de estado-espacio es un conjunto de ecuaciones matriciales que describen como el sistema evoluciona en el tiempo. Estas ecuaciones muestran el cambio en el estado \(\dot{\mathbf{x}}\), y el output \(\mathbf{y}\), para combinaciones lineales del estado actual del vector \(\mathbf{x}\) y input vector \(\mathbf{u}\).
El control del estado-espacio puede soportar sistemas de tiempo continuo y discreto. En el caso de tiempo continuo, la tasa de cambio del estado del sistema \(\mathbf{\dot{x}}\) es expresado como una combinación lineal el estado actual \(\mathbf{x}\) y entrada \(\mathbf{u}\).
En contraste, los sistemas de tiempo discreto expresan el estado del sistema en nuestro siguiente paso del tiempo \(\mathbf{x}_{k+1}\) basado en el estado actual \(\mathbf{x}_k\) y la entrada \(\mathbf{u}_k\), donde \(k\) es el paso de tiempo actual y \(k+1\) es el siguiente paso de tiempo.
Tanto en la forma de tiempo continuo como en la discreta, el vector salida \(\mathbf{y}\) se expresa como una combinación lineal del estado y entrada actual. En muchos casos, la salida es un subconjunto de estados del sistema, y no tiene contribución de la entrada actual.
Cuando modelamos el sistema, primero derivamos la representación del tiempo continuo poruqe las ecuaciones de movimiento son naturalmente escritas como la tasa de cambio de un estado del sistema como una combinación lineal del actual estado y las entradas. Convertimos la representación a tiempo discreto en el robot porque actualizamos el sistema en pasos de tiempo discretos ahí en vez de continuamente.
Los siguientes dos conjuntos de ecuaciones son la forma estándar de la notación estado-espacio del tiempo continuo y tiempo discreto:
Un sistema de estado-espacio con tiempo continuo puede ser convertido en un sistema de tiempo discreto mediante un proceso llamado discretización.
Nota
En la forma de tiempo discreto, el estado del sistema es mantenido constantemente mediante actualizaciones. Esto significa que solo podemos reaccionar a los disturbios tan rápido como nuestra estimación de estado sea actualizada. Actualizando nuestra estimación más rápido puede ayudar a mejorar la actuación, hasta un punto. La clase Notifier de WPILib se puede utilizar si se desean actualizaciones más rápidas que el bucle principal del robot.
Nota
Mientras que las matrices A, B, C y D de tiempo continuo y discreto de un sistema tengan los mismos nombres, no son equivalentes. Las matrices de tiempo continuo describen la tasa de cambio del estado, \(\mathbf{x}\), mientras que las matrices de tiempo discreto describen el estado del sistema en el siguiente paso de tiempo como una función del estado actual y la entrada.
Importante
El Sistema lineal de WPILib toma las matrices del sistema de tiempo continuo, y las convierte internamente al tiempo discreto donde sea necesario.
State-space Notation Example: Flywheel from Kv and Ka
Recall that we can model the motion of a flywheel connected to a brushed DC motor with the equation \(V = K_v \cdot v + K_a \cdot a\), where V is voltage output, v is the flywheel’s angular velocity and a is its angular acceleration. This equation can be rewritten as \(a = \frac{V - K_v \cdot v}{K_a}\), or \(a = \frac{-K_v}{K_a} \cdot v + \frac{1}{K_a} \cdot V\). Notice anything familiar? This equation relates the angular acceleration of the flywheel to its angular velocity and the voltage applied.
Podemos convertir esta ecuación a notación estado-espacio. Podemos crear un sistema con un estado (velocidad), una entrada (voltaje), y una salida (velocidad). Recuerde que la primera derivada de la velocidad es la aceleración, podemos escribir nuestra ecuación como sigue, reemplazando velocidad con \(\mathbf{x}\), aceleración con \(\mathbf{\dot{x}}\), y voltaje \(\mathbf{V}\) con \(\mathbf{u}\):
The output and state are the same, so the output equation is the following:
That’s it! That’s the state-space model of a system for which we have the \(K_v\) and \(K_a\) constants. This same math is used in system identification to model flywheels and drivetrain velocity systems.
Visualizando las Respuestas del Estado-Espacio: Retrato de Fase
A phase portrait can help give a visual intuition for the response of a system in state-space. The vectors on the graph have their roots at some point \(\mathbf{x}\) in state-space, and point in the direction of \(\mathbf{\dot{x}}\), the direction that the system will evolve over time. This example shows a model of a pendulum with the states of angle and angular velocity.
Para trazar una trayectoria potencial que un sistema puede tomar por el estado-espacio, escoja un punto para empezar y siga las flechas alrededor. En éste ejemplo, empezaremos en \([-2, 0]\). Desde aquí, la velocidad aumenta como se balancea verticalmente y empieza a reducir hasta que alcanza el extremo opuesto del columpio. Este ciclo de giro sobre el origen se repite indefinidamente.
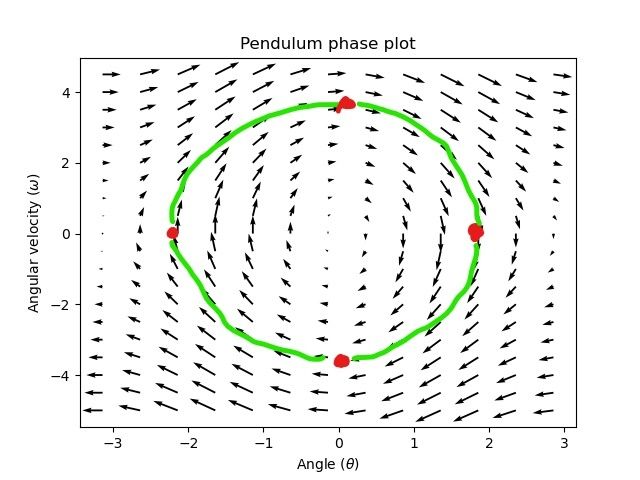
Note que cerca de los bordes del retrato de fase, el eje X se envuelve como una rotación de \(\pi\) radianes en sentido de las manecillas del reloj y una rotación de \(\pi\) radianes en sentido de las manecillas del reloj terminará con el mismo punto.
Para más en ecuaciones diferenciales y retratos de fase, vea el video de 3Blue1Brown Ecuaciones Diferenciales – hacen un gran trabajo de animación de la fase del péndulo alrededor del 15:30.
Visualizando Feedfoward
Este retrato de fase muestra las respuestas de «bucle abierto» del sistema, es decir, cómo reaccionará si dejamos que el estado evolucione naturalmente. Si queremos, digamos, equilibrar el péndulo horizontal (en \((\frac{\pi}{2}, 0)\) en el espacio de estados), necesitaríamos aplicar de alguna manera un control input para contrarrestar la tendencia de bucle abierto del péndulo a oscilar hacia abajo. Esto es lo que el feedforward está tratando de hacer: hacerlo de manera que nuestro retrato de fase tenga un equilibrio en la posición de reference (o punto de ajuste) en el espacio de estado.
Looking at our phase portrait from before, we can see that at \((\frac{\pi}{2}, 0)\) in state space, gravity is pulling the pendulum down with some torque T, and producing some downward angular acceleration with magnitude \(\frac{\tau}{I}\), where I is angular moment of inertia of the pendulum. If we want to create an equilibrium at our reference of \((\frac{\pi}{2}, 0)\), we would need to apply an input can counteract the system’s natural tendency to swing downward. The goal here is to solve the equation \(\mathbf{0 = Ax + Bu}\) for \(\mathbf{u}\). Below is shown a phase portrait where we apply a constant input that opposes the force of gravity at \((\frac{\pi}{2}, 0)\):
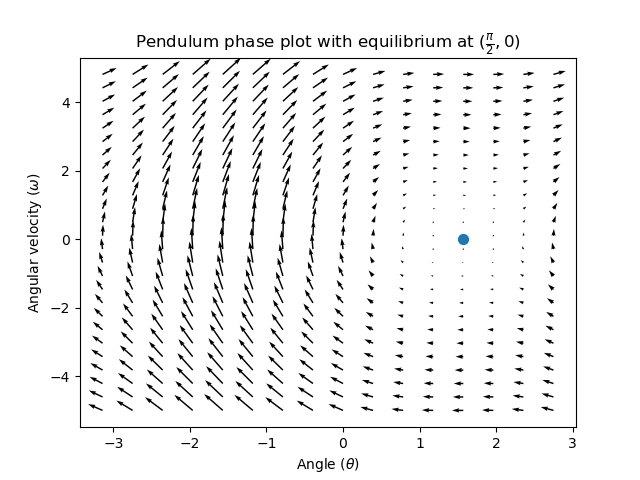
Control de Retroalimentación
En el caso de los motores de control directo, con solo un modelo matemático y conocimiento de todos los estados actuales del sistema (ej. velocidad angular), podemos predecir todos los futuros estados dados en las entradas de futuros voltajes. Pero si el sistema es cambiado en alguna manera que no esté modelada por nuestras ecuaciones, como una carga o fricción inesperada, la velocidad angular del motor va a derivar del modelo por el tiempo. Para combatir esto, podemos dar al motor comandos correctivos usando el controlador de retroalimentación.
Un controlador de PID es una forma de control de retroalimentación. El control del estado-espacio usa la siguiente ley de control, donde \(\mathbf{K}\) es algún controlador de matriz de ganancia, \(\mathbf{r}\) es un estado de referencia, y \(\mathbf{x}\) es el estado actual en estado-espacio. La diferencia entre estos dos vectores, \(\mathbf{r-x}\), es el error.
Esta ley de control es un controlador proporcional para cada estado del sistema. Controladores proporcionales crean resortes definidos por el software que empujan nuestro estado del sistema hacia nuestro estado de referencia en el estado-espacio. En el caso de que el sistema siendo controlado tenga estados de posición y velocidad, la ley de control de arriba como un controlador PD, que también intenta llevar al error de posición y velocidad a cero.
Veamos un ejemplo de esta ley de control en acción. Usaremos un sistema de péndulo desde abajo. donde el péndulo balanceante rodea al origen en estado-espacio. El caso donde \(\mathbf{K}\) es la matriz cero (una matriz con todos cero) escogería las ganancias P y D de cero – no se aplicaría entrada de control, y el retrato de fase va a verse idéntico al de arriba.
Para añadir algo de retroalimentación, arbitrariamente escogemos \(\mathbf{K}\) of [2, 2], donde nuestra entrada al péndulo es la aceleración angular. Esta K significará que por cada radian de posición error, la aceleración angular será 2 radianes por segundo cuadrado; similarmente, aceleramos por 2 radianes por segundo cuadrado por cada radian por segundo de error. Intente seguir una flecha desde algún punto en el estado-espacio hacia adentro – no importa las condiciones iniciales, el estado sentará en la referencia en vez de rodear sin fin con feedforward pura.
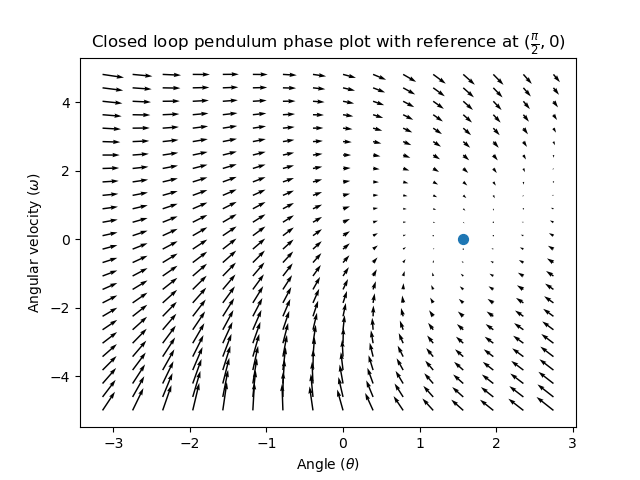
¿Pero cómo podemos elegir una matriz K optima de ganancia para nuestro sistema? Mientras podemos manualmente elegir las ganancias y simular la respuesta del sistema o sintonizarlo en el robot como controlador PID, la teoría de control moderna tiene mejor respuesta: el Regulador Lineal Cuadrático (LQR, en inglés)
El Regulador Lineal Cuadrático
Ya que el control basado en modelo significa que podemos predecir los futuros estados del sistema dada la condición inicial y las entradas de control futuras, podemos tomar una matriz matemática óptima de ganancia \(\mathbf{K}\). Para hacer esto, primero tenemos que definir que tan «bien» o «mal» \(\mathbf{K}\) se vería. Hacemos esto sumando el cuadrado del error y entrada de control con el paso del tiempo, que nos da un número representado que tan «mal» será nuestra ley de control. Si minimizamos la suma, llegaremos a la ley de control óptima.
LQR: Definición
Linear-Quadratic Regulators work by finding a control law that minimizes the following cost function, which weights the sum of error and control effort over time, subject to the linear system dynamics \(\mathbf{x_{k+1} = Ax_k + Bu_k}\).
The control law that minimizes \(\mathbf{J}\) can be written as \(\mathbf{u = K(r_k - x_k)}\), where \(r_k - x_k\) is the error.
Nota
Las matrices de diseño \(\mathbf{Q}\) y \(\mathbf{R}\) de LQR no necesitan discretización, pero \(\mathbf{K}\) calcula por tiempo continuo y discreto systems será diferente.
LQR: Afinación
Como los controladores PID pueden ser afinados ajustando sus ganancias, también queremos cambiar como la ley de control balancea el error y la entrada. Por ejemplo, la nave puede querer minimizar el combustible que expande para alcanzar una referencia dada, mientras que un brazo robótico a alta velocidad puede necesitar reaccionar rápidamente a las alteraciones.
Podemos pesar el esfuerzo del error y control de nuestro LQR con las matrices \(\mathbf{Q}\) y \(\mathbf{R}\). En nuestra función de costo (que describe que tan «mal» nuestra ley de control actuará), \(\mathbf{Q}\) y \(\mathbf{R}\) pesa nuestro error y entrada de control relativo a cada uno. En nuestro ejemplo del cohete de arriba, podemos usar \(\mathbf{Q}\) con números relativamente pequeños para mostrar que no queremos penalizar altamente el error, mientras
Con WPILib, las clases de LQR toman el vector de las excursiones de estado máximo deseado y esfuerzos de control y los convierte internamente a unas matrices completas Q y R con la regla de Bryson. Usualmente usamos el caso menor de \(\mathbf{q}\) y \(\mathbf{r}\) para referirse a esos vectores, y \(\mathbf{Q}\) and \(\mathbf{R}\) para referirse a las matrices.
Increasing the \(\mathbf{q}\) elements would make the LQR less heavily weight large errors, and the resulting control law will behave more conservatively. This has a similar effect to penalizing control effort more heavily by decreasing \(\mathbf{r}\)'s elements.
Similarly, decreasing the \(\mathbf{q}\) elements would make the LQR penalize large errors more heavily, and the resulting control law will behave more aggressively. This has a similar effect to penalizing control effort less heavily by increasing \(\mathbf{r}\) elements.
Por ejemplo, podríamos usar el siguiente Q y R para un sistema de elevador con estados de posición y velocidad.
// Example system -- must be changed to match your robot.
LinearSystem<N2, N1, N1> elevatorSystem = LinearSystemId.identifyPositionSystem(5, 0.5);
LinearQuadraticRegulator<N2, N1, N1> controller = new LinearQuadraticRegulator(elevatorSystem,
// q's elements
VecBuilder.fill(0.02, 0.4),
// r's elements
VecBuilder.fill(12.0),
// our dt
0.020);
// Example system -- must be changed to match your robot.
LinearSystem<2, 1, 1> elevatorSystem = frc::LinearSystemId::IdentifyVelocitySystem(5, 0.5);
LinearQuadraticRegulator<2, 1> controller{
elevatorSystem,
// q's elements
{0.02, 0.4},
// r's elements
{12.0},
// our dt
0.020_s};
from wpimath.controller import LinearQuadraticRegulator_2_1
from wpimath.system.plant import LinearSystemId
# Example system -- must be changed to match your robot.
elevatorSystem = LinearSystemId.identifyPositionSystemMeters(5, 0.5)
controller = LinearQuadraticRegulator_2_1(
elevatorSystem,
# q's elements
(0.02, 0.4),
# r's elements
(12.0,),
# our dt
0.020,
)
LQR: ejemplo de aplicación
Let’s apply a Linear-Quadratic Regulator to a real-world example. Say we have a flywheel velocity system determined through system identification to have \(K_v = 1 \frac{\text{volts}}{\text{radian per second}}\) and \(K_a = 1.5 \frac{\text{volts}}{\text{radian per second squared}}\). Using the flywheel example above, we have the following linear system:
Arbitrariamente escogemos la excursión del estado deseado (error máximo) de \(q = [0.1\ \text{rad/seg}]\), y un \(\mathbf{r}\) de \([12\ \text{volts}]\). Después de la discretización con paso de 20ms, encontramos una ganancia de \(\mathbf{K} = ~81\). Esta ganancia K actúa como el componente proporcional del bucle PID en la velocidad del volante.
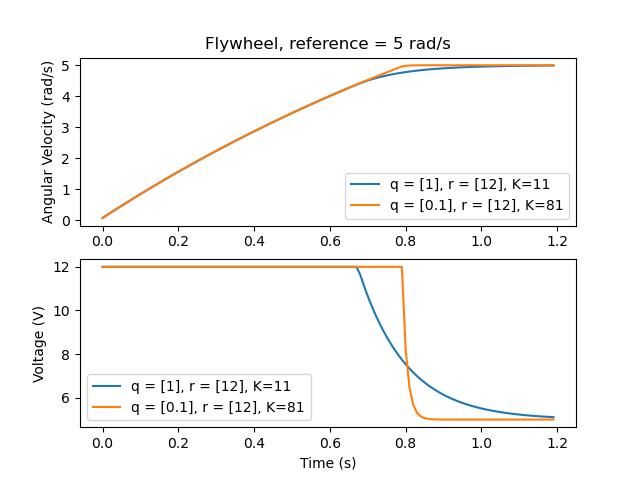
Let’s adjust \(\mathbf{q}\) and \(\mathbf{r}\). We know that increasing the q elements or decreasing the \(\mathbf{r}\) elements we use to create \(\mathbf{Q}\) and \(\mathbf{R}\) would make our controller more heavily penalize control effort, analogous to trying to driving a car more conservatively to improve fuel economy. In fact, if we increase our error tolerance q from 0.1 to 1.0, our gain matrix \(\mathbf{K}\) drops from ~81 to ~11. Similarly, decreasing our maximum voltage \(r\) from 12.0 to 1.2 decreases \(\mathbf{K}\).
La siguiente gráfica muestra la velocidad angular del volante y el voltaje aplicado en el tiempo con dos diferentes ganancias. Podemos ver como una ganancia más alta puede hacer que el sistema alcance la referencia más rápido (a t = 0.8 segundos), mientras dejamos nuestro motor saturado a 12V por más tiempo. Es igual a incrementar la ganancia P de un controlador PID por un factor de ~8x.
LQR y Medición de Compensación de Latencia
La mayoría del tiempo, nuestros sensores tienen un retraso asociado con sus medidas. Por ejemplo el controlador de motor SPARK MAX sobre CAN puede tener 30ms de retraso asociado con las mediciones de velocidad.
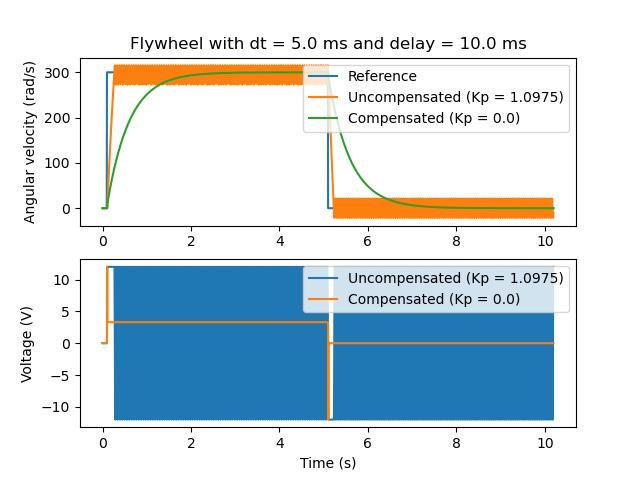
Este retraso significa que nuestro controlador de retroalimentación va a estar generando comandos de voltaje basados en estimaciones de estado del pasado. Regularmente tiene el efecto de introducir inestabilidad y oscilaciones en el sistema, como se muestra en la gráfica de abajo.
However, we can model our controller to control where the system’s state is delayed into the future. This will reduce the LQR’s gain matrix \(\mathbf{K}\), trading off controller performance for stability. The below formula, which adjusts the gain matrix to account for delay, is also used in system identification.
Multiplicando \(\mathbf{K}\) por \(\mathbf{A} - \mathbf{BK}\) esencialmente avanza las ganancias por un paso de tiempo. En este caso, multiplicamos por \(\left(\mathbf{A} - \mathbf{BK}\right)^{\text{delay} / dt}\) para avanzar las ganancias por el retraso de las mediciones.
Nota
Esto puede tener efecto de reducir \(\mathbf{K}\) a cero, de manera efectiva inhabilitando el control de retroalimentación.
Nota
El controlador de motor SPARK MAX utiliza un filtro FIR de 40 tomas con un retraso de 19,5 ms, y los marcos de estado se envían por defecto cada 20 ms.
El siguiente código muestra cómo ajustar la ganancia K del controlador LQR para los retardos de entrada del sensor:
// Adjust our LQR's controller for 25 ms of sensor input delay. We
// provide the linear system, discretization timestep, and the sensor
// input delay as arguments.
controller.latencyCompensate(elevatorSystem, 0.02, 0.025);
// Adjust our LQR's controller for 25 ms of sensor input delay. We
// provide the linear system, discretization timestep, and the sensor
// input delay as arguments.
controller.LatencyCompensate(elevatorSystem, 20_ms, 25_ms);
# Adjust our LQR's controller for 25 ms of sensor input delay. We
# provide the linear system, discretization timestep, and the sensor
# input delay as arguments.
controller.latencyCompensate(elevatorSystem, 0.020, 0.025)
Linealización
La linealización es una herramienta usada para aproximar las funciones no lineales y el sistema de estado-espacio usando las lineales. En el espacio bidimensional, las funciones lineales son líneas derechas mientras las funciones no lineales son curvas. Un ejemplo común de la función no lineal y correspondiente aproximación lineal es \(y=\sin{x}\). Esta función puede estar aproximada por \(y=x\) cercano a cero. Esta aproximación es precisa mientras esté cerca de \(x=0\), pero pierde la precisión mientras más nos alejamos del punto de linealización. Por ejemplo, la aproximación \(\sin{x} \approx x\) es precisa a 0.02 - 0.5 radianes de \(y = 0\), pero rápidamente pierde la precisión después de eso. La siguiente imagen, podemos ver:math:y =sin{x}, \(y=x\) y la diferencia entre la aproximación y el valor real de \(\sin{x}\) en \(x\).
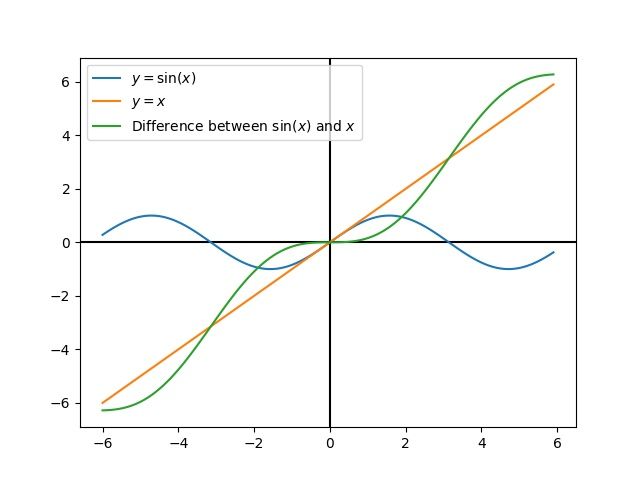
Podemos también linealizar el sistema estado-espacio con dinámicas no lineales. Hacemos esto eligiendo un punto \(\mathbf{x}\) en el estado-espacio y usando esto como entrada para nuestras funciones no lineales. Como el ejemplo de arriba, esto funciona bien para los estados cerca del punto sobre el cual se linealiza el sistema, pero podemos divergir rápidamente lejos de ese estado.