Observadores de estado y filtros de Kalman
Los observadores de estados combinan información sobre el comportamiento de un sistema y mediciones externas para estimar el verdadero estado del sistema. Un observador común utilizado para sistemas lineales es el filtro de Kalman. Los filtros de Kalman son ventajosos sobre otros filtros ya que fusionan las mediciones de uno o más sensores con un modelo de espacio de estado del sistema para estimar de manera óptima el estado de un sistema.
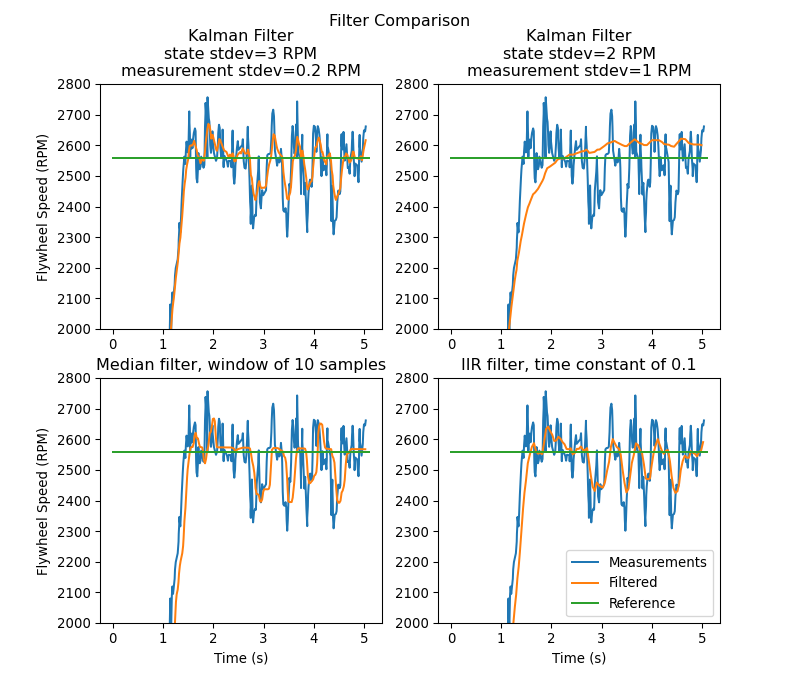
Esta imagen muestra las mediciones de la velocidad del volante a lo largo del tiempo, ejecutadas a través de una variedad de filtros diferentes. Tenga en cuenta que un filtro de Kalman bien ajustado no muestra ningún retraso de medición durante el giro del volante, mientras que sigue rechazando datos ruidosos y reacciona rápidamente a las perturbaciones cuando las bolas pasan a través de él. Puede encontrar más información sobre filtros en sección de filtros .
Funciones gaussianas
Kalman filters utilize a Gaussian distribution to model the noise in a process [1]. In the case of a Kalman filter, the estimated state of the system is the mean, while the variance is a measure of how certain (or uncertain) the filter is about the true state.

La idea de varianza y covarianza es fundamental para la función de un filtro de Kalman. La covarianza es una medida de cómo se correlacionan dos variables aleatorias. En un sistema con un solo estado, la matriz de covarianza es simplemente \(\ mathbf {\ text {cov} (x_1, x_1)}\), o una matriz que contiene la varianza:math:mathbf {text {var } (x_1)} `del estado: matemáticas: x_1`. La magnitud de esta varianza es el cuadrado de la desviación estándar de la función gaussiana que describe la estimación del estado actual. Los valores relativamente grandes de covarianza pueden indicar datos ruidosos, mientras que las pequeñas covarianzas pueden indicar que el filtro tiene más confianza en su estimación. Recuerde que los valores «grandes» y «pequeños» para la varianza o covarianza son relativos a la unidad base que se está utilizando, por ejemplo, si \(\ mathbf{x_1}\) se midió en metros, \(\mathbf{\text{cov}(x_1, x_1)}\) estaría en metros al cuadrado.
Las matrices de covarianza se escriben de la siguiente forma:
Filtros de Kalman
Importante
Es importante desarrollar una intuición de lo que realmente hace un filtro de Kalman. El libro Kalman and Bayesian Filters in Python de Roger Labbe <https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python> __ proporciona una excelente introducción visual e interactiva a los filtros bayesianos. Los filtros de Kalman en WPILib usan álgebra lineal para gentrificar las matemáticas, pero las ideas son similares al caso unidimensional. Sugerimos leer el Capítulo 4 para hacerse una idea de lo que hacen estos filtros.
To summarize, Kalman filters (and all Bayesian filters) have two parts: prediction and correction. Prediction projects our state estimate forward in time according to our system’s dynamics, and correct steers the estimated state towards the measured state. While filters often perform both in the same timestep, it’s not strictly necessary – For example, WPILib’s pose estimators call predict frequently, and correct only when new measurement data is available (for example, from a low-framerate vision system).
A continuación se muestran las ecuaciones de un filtro de Kalman de tiempo discreto:
La estimación del estado \(\mathbf {x}\), junto con \(\mathbf{P}\), describe la media y la covarianza de la función gaussiana que describe la estimación de nuestro filtro del estado verdadero del sistema.
Matrices de covarianza de proceso y medición de ruido
Las matrices de covarianza de ruido de proceso y medición \(\mathbf{Q}\) y \(\mathbf{R}\) describen la varianza de cada uno de nuestros estados y medidas. Recuerde que para una función gaussiana, la varianza es el cuadrado de la desviación estándar de la función. En un WPILib, Q y R son matrices diagonales cuyas diagonales contienen sus respectivas varianzas. Por ejemplo, un filtro de Kalman con estados: matemáticas begin{bmatrix}text{position} \ text{velocity} end{bmatrix} y medidas \(\begin{bmatrix}\text{position} \end{bmatrix}\) con desviaciones de estado estándar \(\begin{bmatrix}0.1 \\ 1.0\end{bmatrix}\) y desviación estándar de medición \(\begin{bmatrix}0.01\end{bmatrix}\) tendría las siguientes \(\mathbf{Q}\) y \(\mathbf{R}\) matrices:
Matriz de covarianza de errores
La matriz de covarianza de error \(\mathbf{P}\) describe la covarianza de la estimación del estado \(\mathbf{\hat{x}}\). De manera informal, \(\mathbf{P}\) describe nuestra certeza sobre el estado estimado. Si \(\mathbf{P}\) es grande, nuestra incertidumbre sobre el estado real es grande. A la inversa, a \(\mathbf{P}\) con elementos más pequeños implicaría menos incertidumbre sobre nuestro verdadero estado.
A medida que proyectamos el modelo hacia adelante, :math:mathbf{P}` aumenta a medida que disminuye nuestra certeza sobre el verdadero estado del sistema.
Predecir paso
En la predicción, nuestra estimación de estado se actualiza de acuerdo con la dinámica del sistema lineal \(\mathbf{\dot{x} = Ax + Bu}\). Además, nuestra covarianza de error \(\mathbf{P}\) aumenta por la matriz de covarianza de ruido del proceso \(\mathbf{Q}\). Los valores más grandes de \(\mathbf{Q}\) harán que nuestra covarianza de error \(\mathbf{P}\) crezca más rápidamente. Esto \(\mathbf{P}\) se usa en el paso de corrección para ponderar el modelo y las medidas.
Paso correcto
En el paso correcto, nuestra estimación de estado se actualiza para incluir nueva información de medición. Esta nueva información se pondera contra la estimación del estado \(\mathbf{\hat{x}}\) por la ganancia de Kalman \(\mathbf{K}\). Los valores grandes de \(\mathbf{K}\) ponderan más las medidas entrantes, mientras que los valores más pequeños de \(\mathbf{K}\) ponderan más nuestra predicción de estado. Porque \(\mathbf{K}\) está relacionado con \(\mathbf{P}\), los valores más grandes de \(\mathbf{P}\) aumentarán \(\mathbf{K}\) y medidas más pesadas. Si, por ejemplo, se predice un filtro para una duración prolongada, el grande \(\mathbf{P}\) ponderaría mucho la nueva información.
Finalmente, la covarianza de error \(\mathbf{P}\) disminuye para aumentar nuestra confianza en la estimación del estado.
Ajuste de los filtros de Kalman
Los constructores de las clases de filtros Kalman de WPILib toman un sistema lineal, un vector de desviaciones estándar de ruido de proceso y desviaciones estándar de ruido de medición. Éstos se convierten en matrices \(\mathbf{Q}\) y \(\mathbf{R}\) llenando las diagonales con el cuadrado de las desviaciones estándar, o varianzas, de cada estado o medida. Al disminuir la desviación estándar de un estado (y por lo tanto su entrada correspondiente en \(\mathbf{Q}\)), el filtro desconfiará más de las mediciones entrantes. De manera similar, aumentar la desviación estándar de un estado confiará más en las mediciones entrantes. Lo mismo se aplica a las desviaciones estándar de la medición: disminuir una entrada hará que el filtro confíe más en la medición entrante para el estado correspondiente, mientras que aumentarla disminuirá la confianza en la medición.
48 // The observer fuses our encoder data and voltage inputs to reject noise.
49 private final KalmanFilter<N1, N1, N1> m_observer =
50 new KalmanFilter<>(
51 Nat.N1(),
52 Nat.N1(),
53 m_flywheelPlant,
54 VecBuilder.fill(3.0), // How accurate we think our model is
55 VecBuilder.fill(0.01), // How accurate we think our encoder
56 // data is
57 0.020);
5#include <numbers>
6
7#include <frc/DriverStation.h>
8#include <frc/Encoder.h>
9#include <frc/TimedRobot.h>
10#include <frc/XboxController.h>
11#include <frc/controller/LinearQuadraticRegulator.h>
12#include <frc/drive/DifferentialDrive.h>
13#include <frc/estimator/KalmanFilter.h>
14#include <frc/motorcontrol/PWMSparkMax.h>
15#include <frc/system/LinearSystemLoop.h>
16#include <frc/system/plant/DCMotor.h>
17#include <frc/system/plant/LinearSystemId.h>
18#include <units/angular_velocity.h>
48 // The observer fuses our encoder data and voltage inputs to reject noise.
49 frc::KalmanFilter<1, 1, 1> m_observer{
50 m_flywheelPlant,
51 {3.0}, // How accurate we think our model is
52 {0.01}, // How accurate we think our encoder data is
53 20_ms};
48 # The observer fuses our encoder data and voltage inputs to reject noise.
49 self.observer = wpimath.estimator.KalmanFilter_1_1_1(
50 self.flywheelPlant,
51 [3], # How accurate we think our model is
52 [0.01], # How accurate we think our encoder data is
53 0.020,
54 )