Filtros Lineales
El primer tipo (y más comúnmente empleado) de filtros que WPILib admite es el filtro lineal o, más específicamente un filtro lineal invariante en el tiempo (LTI).
An LTI filter is, put simply, a weighted moving average - the value of the output stream at any given time is a localized, weighted average of the inputs near that time. The difference between different types of LTI filters is thus reducible to the difference in the choice of the weighting function (also known as a «window function» or an «impulse response») used. The mathematical term for this operation is convolution.
Hay dos amplios tipos de respuestas de impulso: respuesta infinita de impulsos (IIR) y respuesta finita de impulsos (FIR).
Las respuestas infinitas de impulsos tiene un «apoyo» infinito - esto es, ellas son distintas a cero en una región infinitamente grande. Esto significa, que también tienen «memoria» infinita – cuando un valor aparece en el flujo de entrada este influirá en todas las salidas subsecuentes, para siempre. Esto es típicamente indeseable desde una perspectiva estricta de procesamiento de señales, sin embargo los filtros con respuestas infinitas de impulsos tienden calcularse fácilmente, ya que se pueden expresar mediante relaciones de recursión simples.
Las respuestas finitas de impulsos tiene un «apoyo» finito – es decir, las respuestas son distintas a cero en una región definida. El «arquetipo» del filtro FIR es un promedio móvil plano – es decir, configurando la salida igual al promedio de n entradas pasadas. Los filtros FIR tienden a tener propiedades más deseadas que los filtros IIR, pero son más complicados para calcular.
Linear filters are supported in WPILib through the LinearFilter class (Java, C++, , Python).
Crear un Filtro Lineal
Nota
La clase C++ LinearFilter se basa en el tipo de información usada en el entrada.
Nota
Debido a que los filtros tienen «memoria», cada flujo de entrada requiere su propio objeto de filtro. No intente usar el mismo objeto de filtro para múltiples flujos de entradas.
Mientras sea posible instanciar directamente la clase LinearFilter para construir un filtro personalizado, es mucho más conveniente (y común) usar uno de los Factory methods suministrados, en su lugar:
singlePoleIIR
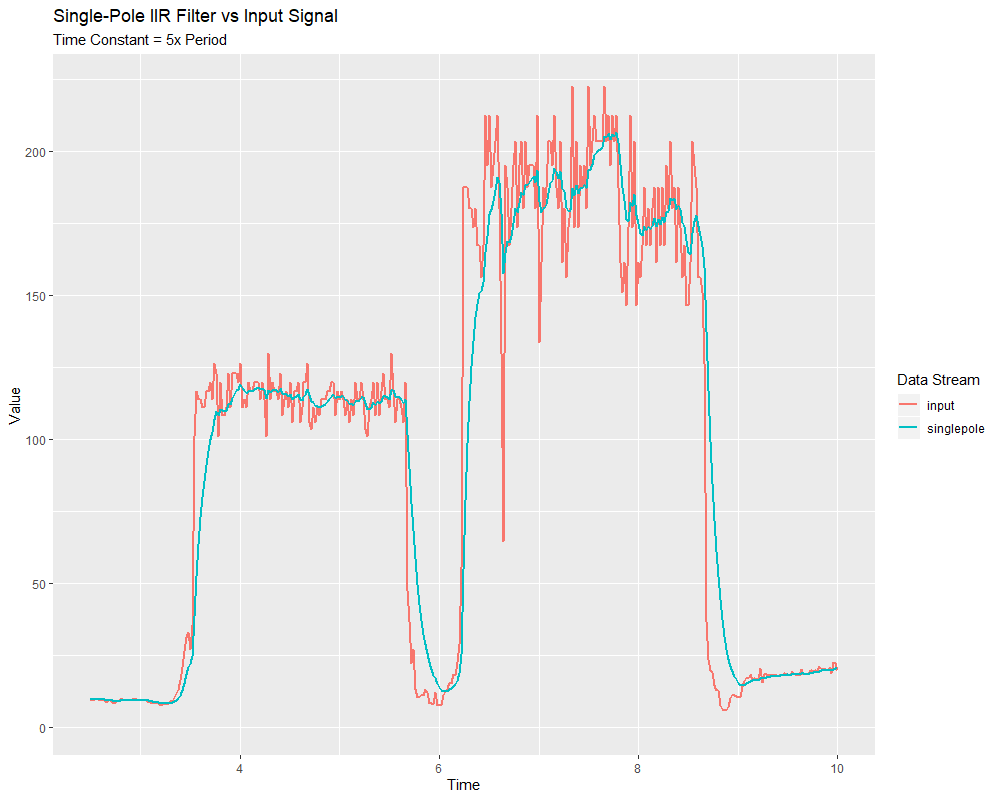
The singlePoleIIR() factory method creates a single-pole infinite impulse response filter which performs exponential smoothing. This is the «go-to,» «first-try» low-pass filter in most applications; it is computationally trivial and works in most cases.
// Creates a new Single-Pole IIR filter
// Time constant is 0.1 seconds
// Period is 0.02 seconds - this is the standard FRC main loop period
LinearFilter filter = LinearFilter.singlePoleIIR(0.1, 0.02);
// Creates a new Single-Pole IIR filter
// Time constant is 0.1 seconds
// Period is 0.02 seconds - this is the standard FRC main loop period
frc::LinearFilter<double> filter = frc::LinearFilter<double>::SinglePoleIIR(0.1_s, 0.02_s);
from wpimath.filter import LinearFilter
# Creates a new Single-Pole IIR filter
# Time constant is 0.1 seconds
# Period is 0.02 seconds - this is the standard FRC main loop period
filter = LinearFilter.singlePoleIIR(0.1, 0.02)
El parámetro de la «constante de tiempo» determina la «escala de tiempo característica» del impulso de respuesta del filtro; el filtro cancelará cualquier dinámica que ocurra en la escala de tiempo significativamente menor que esto. Relacionada, también está la escala de tiempo aproximada de la introducción del phase lag. El recíproco de esta escala de tiempo, multiplicado por 2 pi, es la «frecuencia de corte» del filtro.
El parámetro «periodo» es el periodo en el cual el método calculate() del filtro será llamado. Para la mayoría de las implementaciones, esto será el periodo cíclico estándar de 0.02 segundos del main robot.
Media Móvil
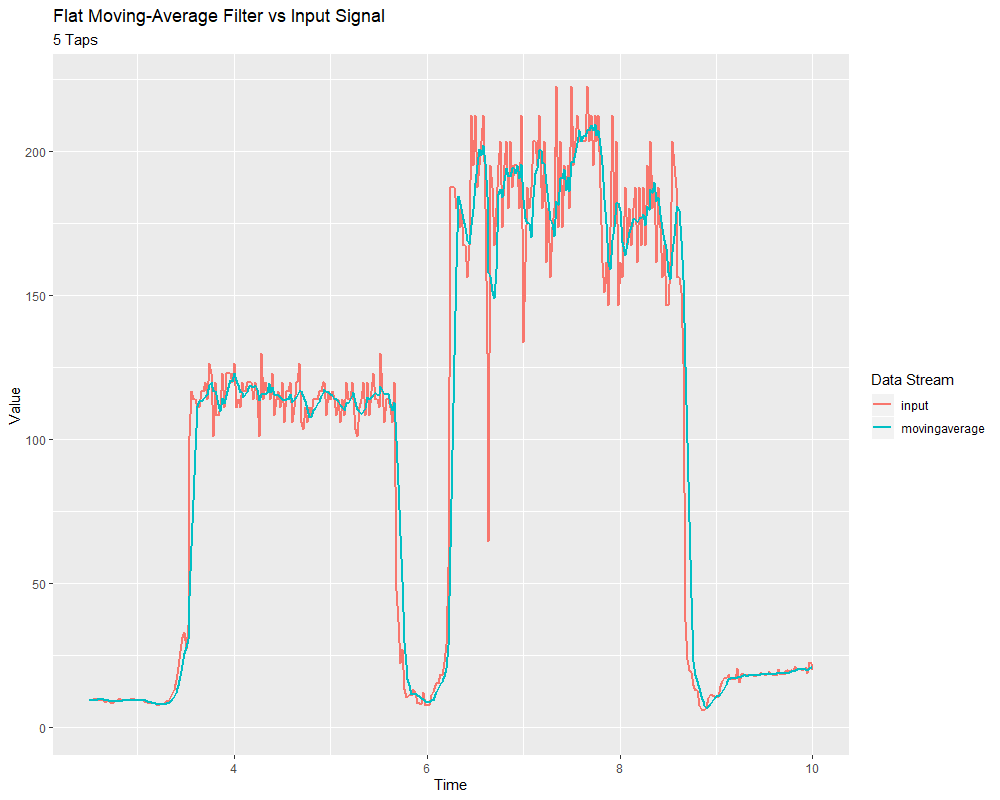
El método de fabrica de media móvil crea un filtro simple de media móvil plana. Este es el filtro paso bajo FIR más simple, y es útil en muchos contextos iguales como los filtros monopolar IIR. Es un poco más complicado de calcular, pero generalmente se comporta de una manera más suave.
// Creates a new flat moving average filter
// Average will be taken over the last 5 samples
LinearFilter filter = LinearFilter.movingAverage(5);
// Creates a new flat moving average filter
// Average will be taken over the last 5 samples
frc::LinearFilter<double> filter = frc::LinearFilter<double>::MovingAverage(5);
from wpimath.filter import LinearFilter
# Creates a new flat moving average filter
# Average will be taken over the last 5 samples
filter = LinearFilter.movingAverage(5)
El parámetro «taps» es el nombre de ejemplos que serán incluidos en la media móvil plana. Esto se comporta similarmente a la «constante de tiempo» anterior – se le llama constante de tiempo efectiva al número de fases de tiempo multiplicado por el periodo en cual calculate() es llamado.
highPass
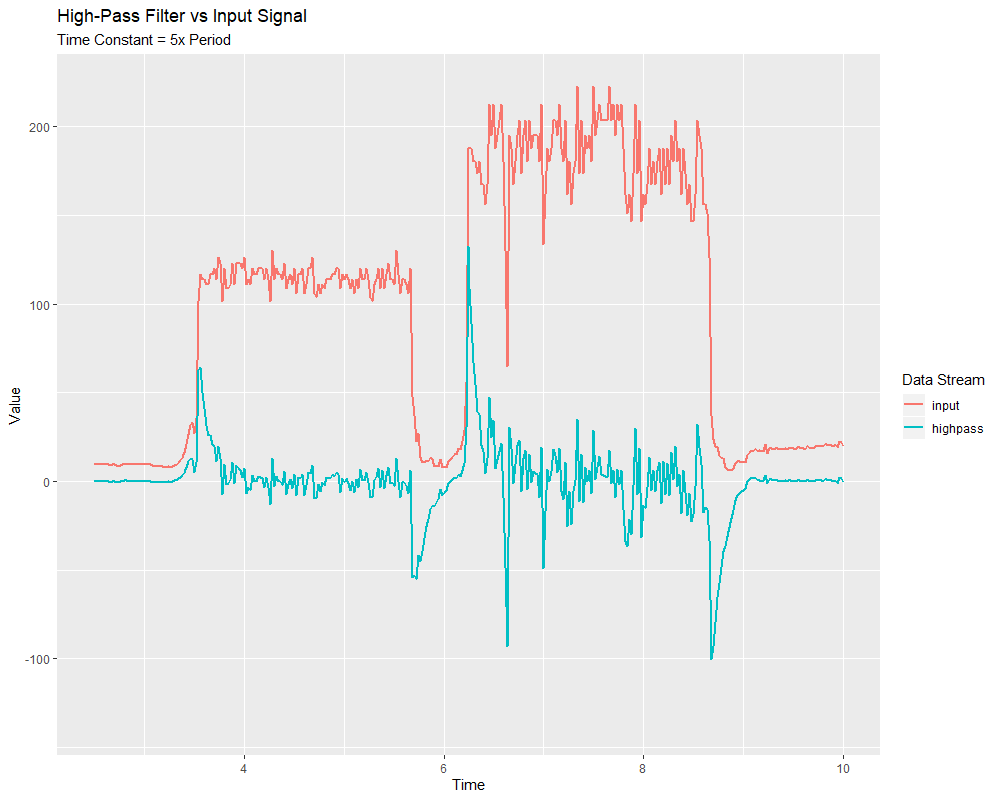
El método de fábrica highPass crea un filtro simple de respuesta de impulso infinita de primer orden. Esto es la «contraparte» del IIR monopolar.
// Creates a new high-pass IIR filter
// Time constant is 0.1 seconds
// Period is 0.02 seconds - this is the standard FRC main loop period
LinearFilter filter = LinearFilter.highPass(0.1, 0.02);
// Creates a new high-pass IIR filter
// Time constant is 0.1 seconds
// Period is 0.02 seconds - this is the standard FRC main loop period
frc::LinearFilter<double> filter = frc::LinearFilter<double>::HighPass(0.1_s, 0.02_s);
from wpimath.filter import LinearFilter
# Creates a new high-pass IIR filter
# Time constant is 0.1 seconds
# Period is 0.02 seconds - this is the standard FRC main loop period
filter = LinearFilter.highPass(0.1, 0.02)
El parámetro de la «constante de tiempo» determina la «escala de tiempo característica» de la respuesta del impulso del filtro; el filtro cancelará cualquier dinámica de la señal que ocurra en la escala de tiempo significativamente más larga que esta. Relacionado, esta también es la escala de tiempo aproximada del phase lead introducida. El recíproco de esta escala de tiempo, multiplicado por 2 pi, es la «frecuencia de corte» del filtro.
El parámetro «periodo» es el periodo en el cual el método calculate() del filtro será llamado. Para la mayoría de las implementaciones, esto será el periodo cíclico estándar de 0.02 segundos del main robot.
Usando un filtro Lineal
Nota
En orden para que el filtro creado obedezca el parámetro de tiempo de escala especificado, la función calculate() deberá ser llamada constantemente en el periodo especificado. Si, por alguna razón, un lapso significante en calculate() debe ocurrir, el método de reset() del filtro deberá ser llamado antes para su uso futuro.
Una vez que su filtro sea creado, usarlo es fácil – solamente llame el método calculate() con la entrada más reciente para obtener la salida filtrada.
// Calculates the next value of the output
filter.calculate(input);
// Calculates the next value of the output
filter.Calculate(input);
# Calculates the next value of the output
filter.calculate(input)