Durum denetleyicisi ve Kalman Filtreleri

Durum gözlemcileri, sistemin doğru state nu tahmin etmek için bir sistemin davranışı ve harici ölçümler hakkındaki bilgileri birleştirir. Doğrusal sistemler için kullanılan yaygın bir gözlemci Kalman Filtresidir. Kalman filtreleri diğerlerine göre avantajlıdır filters, bir sistemin durumunu en iyi şekilde tahmin etmek için sistemin durum-uzay modeliyle bir veya daha fazla sensörden alınan ölçümleri birleştirir.

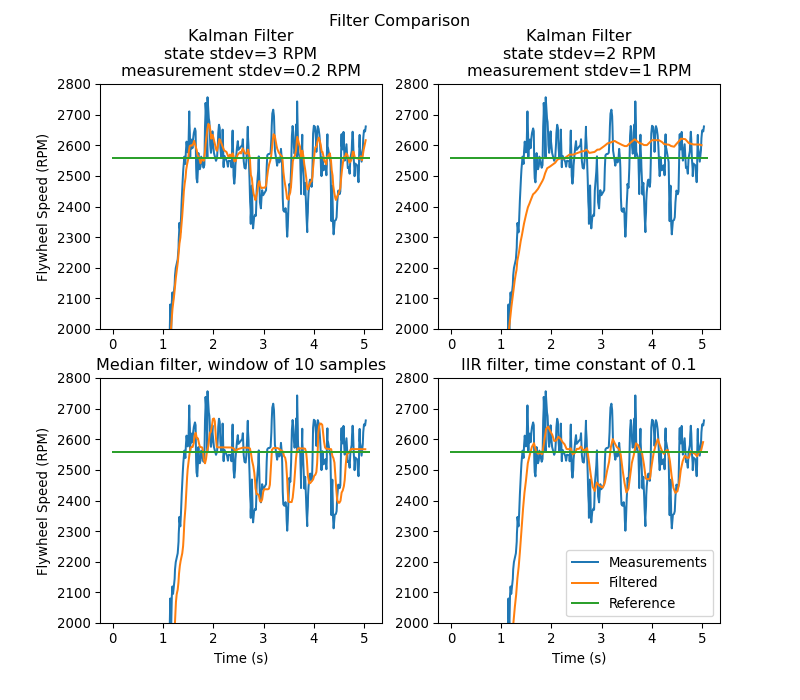
Bu görüntü, çeşitli farklı filtrelerden geçen zaman içindeki dönenteker hızı ölçümlerini gösterir. İyi ayarlanmış bir Kalman filtresinin dönerteker dönüşü sırasında hiçbir ölçüm gecikmesi göstermediğini ve gürültülü verileri hala reddederken ve toplar içinden geçerken rahatsızlıklara hızlı tepki verdiğini unutmayın. Filtrelerle ilgili daha fazla bilgi filters sectionbulunabilir.

Filter comparison between: Kalman, Median, and IIR.

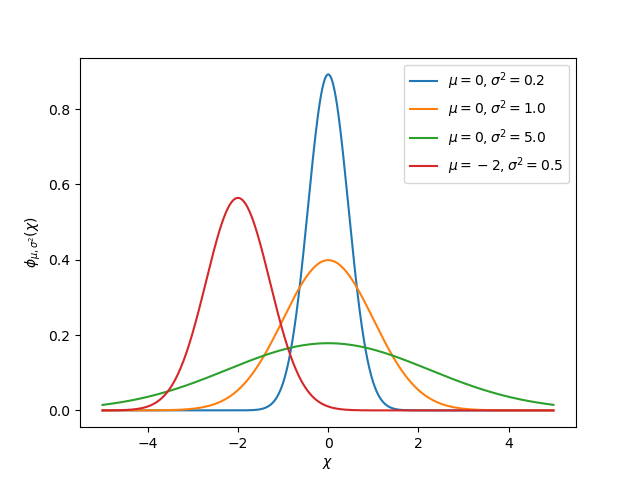
Gauss Fonksiyonları

Kalman filters utilize a Gaussian distribution to model the noise in a process [1]. In the case of a Kalman filter, the estimated state of the system is the mean, while the variance is a measure of how certain (or uncertain) the filter is about the true state.

../../../../_images/normal-distribution.png

Varyans ve kovaryans fikri, bir Kalman filtresinin işlevinin merkezinde yer alır. Kovaryans, iki rastgele değişkenin nasıl ilişkilendirildiğinin bir ölçüsüdür. Tek durumlu bir sistemde kovaryans matrisi basitçe \(\mathbf{\text{var}(x_1)}\) veya varyansı içeren bir matristir \(\mathbf{\text{var}(x_1)}\) durum \(x_1\). Bu varyansın büyüklüğü, mevcut durum tahminini açıklayan Gauss fonksiyonunun standart sapmasının karesidir. Kovaryans için nispeten büyük değerler gürültülü verileri gösterebilirken, küçük kovaryanslar filtrenin tahmini konusunda daha emin olduğunu gösterebilir. Varyans veya kovaryans için “büyük” ve “küçük” değerlerin kullanılan temel birime göre olduğunu unutmayın - örneğin, eğer \(\mathbf{x_1}\) metre cinsinden ölçüldüyse, \(\mathbf{\text{cov}(x_1, x_1)}\) metre kare cinsinden olacaktır.

Kovaryans matrisleri aşağıdaki biçimde yazılır:

\[\begin{split}\mathbf{\Sigma} &= \begin{bmatrix} \text{cov}(x_1, x_1) & \text{cov}(x_1, x_2) & \ldots & \text{cov}(x_1, x_n) \\ \text{cov}(x_2, x_1) & \text{cov}(x_2, x_2) & \ldots & \text{cov}(x_1, x_n) \\ \vdots & \vdots & \ddots & \vdots \\ \text{cov}(x_n, x_1) & \text{cov}(x_n, x_2) & \ldots & \text{cov}(x_n, x_n) \\ \end{bmatrix}\end{split}\]

Kalman Filtreleri

Önemli

Bir Kalman filtresinin gerçekte ne yaptığına dair bir sezgi geliştirmek önemlidir. Kalman and Bayesian Filters in Python by Roger Labbe tarafından kitap Bayes filtrelerine harika bir görsel ve etkileşimli giriş sağlar. WPILib’deki Kalman filtreleri matematiği kolay hale getirmek için doğrusal cebir kullanır, ancak fikirler tek boyutlu duruma benzer. Bu filtrelerin ne yaptığına dair bir fikir edinmek için Bölüm 4’ü okumanızı öneririz.

To summarize, Kalman filters (and all Bayesian filters) have two parts: prediction and correction. Prediction projects our state estimate forward in time according to our system’s dynamics, and correct steers the estimated state towards the measured state. While filters often perform both in the same timestep, it’s not strictly necessary – For example, WPILib’s pose estimators call predict frequently, and correct only when new measurement data is available (for example, from a low-framerate vision system).

Aşağıda, ayrık zamanlı bir Kalman filtresinin denklemleri gösterilmektedir:

\[\begin{split}\text{Predict step} \nonumber \\ \hat{\mathbf{x}}_{k+1}^- &= \mathbf{A}\hat{\mathbf{x}}_k^+ + \mathbf{B} \mathbf{u}_k \\ \mathbf{P}_{k+1}^- &= \mathbf{A} \mathbf{P}_k^- \mathbf{A}^T + \mathbf{\Gamma}\mathbf{Q}\mathbf{\Gamma}^T \\ \text{Update step} \nonumber \\ \mathbf{K}_{k+1} &= \mathbf{P}_{k+1}^- \mathbf{C}^T (\mathbf{C}\mathbf{P}_{k+1}^- \mathbf{C}^T + \mathbf{R})^{-1} \\ \hat{\mathbf{x}}_{k+1}^+ &= \hat{\mathbf{x}}_{k+1}^- + \mathbf{K}_{k+1}(\mathbf{y}_{k+1} - \mathbf{C} \hat{\mathbf{x}}_{k+1}^- - \mathbf{D}\mathbf{u}_{k+1}) \\ \mathbf{P}_{k+1}^+ &= (\mathbf{I} - \mathbf{K}_{k+1}\mathbf{C})\mathbf{P}_{k+1}^-\end{split}\]
\[\begin{split}\begin{array}{llll} \mathbf{A} & \text{system matrix} & \hat{\mathbf{x}} & \text{state estimate vector} \\ \mathbf{B} & \text{input matrix} & \mathbf{u} & \text{input vector} \\ \mathbf{C} & \text{output matrix} & \mathbf{y} & \text{output vector} \\ \mathbf{D} & \text{feedthrough matrix} & \mathbf{\Gamma} & \text{process noise intensity vector} \\ \mathbf{P} & \text{error covariance matrix} & \mathbf{Q} & \text{process noise covariance matrix} \\ \mathbf{K} & \text{Kalman gain matrix} & \mathbf{R} & \text{measurement noise covariance matrix} \end{array}\end{split}\]

Durum tahmini \(\mathbf{x}\), ile birlikte \(\mathbf{P}\), filtremizin sistemin gerçek durumuna ilişkin tahminini tanımlayan Gauss işlevinin ortalamasını ve kovaryansını açıklar.

Gürültü Kovaryans Matrislerinin İşlenmesi ve Ölçümü

Süreç ve ölçüm gürültüsü kovaryans matrisleri \(\mathbf{Q}\) ve:math:mathbf{R} durumlarımızın ve ölçümlerimizin her birinin varyansını tanımlar. Bir Gauss fonksiyonu için varyansın, fonksiyonun standart sapmasının karesi olduğunu unutmayın. Bir WPILib’de Q ve R, köşegenleri ilgili varyanslarını içeren köşegen matrisleridir. Örneğin, \(\begin{bmatrix}\text{position} \\ \text{velocity} \end{bmatrix}\) ve ölçümler \(\begin{bmatrix}\text{position} \end{bmatrix}\) durum standart sapmalarıyla:math:begin{bmatrix}0.1 \ 1.0end{bmatrix} ve ölçüm standart sapması \(\begin{bmatrix}0.01\end{bmatrix}\) şunlara sahip olacaktır \(\mathbf{Q}\) and \(\mathbf{R}\) matrisler:

\[\begin{split}Q = \begin{bmatrix}0.01 & 0 \\ 0 & 1.0\end{bmatrix}, R = \begin{bmatrix}0.0001\end{bmatrix}\end{split}\]

Error Covariance Matrix-Hata Kovaryans Matrisi

Hata kovaryans matrisi \(\mathbf{P}\), durum tahmininin kovaryansını açıklar \(\mathbf{\hat{x}}\). Gayri resmi olarak, \(\mathbf{P}\), tahmin edilen state hakkındaki kesinliğimizi tanımlar. Eğer \(\mathbf{P}\) büyükse, gerçek durum hakkındaki belirsizliğimiz büyüktür. Tersine, daha küçük elemanlara sahip \(\mathbf{P}\), gerçek durumumuz hakkında daha az belirsizlik anlamına gelir.

Modeli ileriye doğru yansıtırken, sistemin gerçek durumu hakkındaki kesinliğimiz azaldıkça \(\mathbf{P}\) artar.

Tahmin adımı

Tahminde, durum tahminimiz doğrusal sistem dinamiklerine göre güncellenir \(\mathbf{\dot{x} = Ax + Bu}\). Ayrıca, hata kovaryansımız \(\mathbf{P}\), işlem gürültü kovaryans matrisi \(\mathbf{Q}\) ile artar. Daha büyük \(\mathbf{Q}\) değerleri, hata kovaryansımızın \(\mathbf{P}\) daha hızlı büyümesini sağlayacaktır. Bu \(\mathbf{P}\), modeli ve ölçümleri ağırlıklandırmak için düzeltme adımında kullanılır.

Doğru adım

Doğru adımda, durum tahminimiz yeni ölçüm bilgilerini içerecek şekilde güncellenir. Bu yeni bilgi, Kalman kazancı \(\mathbf{K}\) tarafından \(\ mathbf{\hat {x}}\) ‘durum tahminine göre ağırlıklandırılır. \(\mathbf{K}\) ‘nın büyük değerleri gelen ölçümleri daha fazla ağırlıklandırırken, \(\mathbf{K}\) ‘nın daha küçük değerleri durum tahminimize daha fazla ağırlık verir. Çünkü \(\mathbf{K}\), \(\mathbf{P}\) ile ilgilidir, \(\mathbf{P}\) ‘nin daha büyük değerleri \(\mathbf{K}' 'yı arttıracaktır ve ölçümleri daha ağırlıklandıracaktır. Örneğin, uzun bir süre için bir filtre tahmin edilirse, büyük :math:\)mathbf{P}`, yeni bilgileri büyük ölçüde ağırlaştıracaktır.

Son olarak, hata kovaryansı \(\mathbf{P}\) durum tahminine olan güvenimizi artırmak için azalır.

Kalman Filtrelerini Ayarlama

WPILib’in Kalman Filtresi sınıflarının constructorları, doğrusal bir sistemi, işlem gürültüsü standart sapmalarının bir vektörünü ve ölçüm gürültüsü standart sapmalarını alır. Bunlar, köşegenleri her durum veya ölçümün standart sapmalarının veya varyanslarının karesiyle doldurarak \(\mathbf{Q}\) ve \(\mathbf{R}\) matrislerine dönüştürülür. Bir durumun standart sapmasını (ve dolayısıyla, \(\mathbf{Q}\) içindeki karşılık gelen girdisini) azaltarak, filtre gelen ölçümlere daha fazla güvenmeyecektir. Benzer şekilde, bir durumun standart sapmasını artırmak, gelen ölçümlere daha çok güvenecektir. Aynısı, ölçüm standart sapmaları için de geçerlidir - bir girişi azaltmak, filtrenin ilgili durum için gelen ölçüme daha fazla güvenmesini sağlarken, artması ölçüme olan güveni azaltacaktır.

48  // The observer fuses our encoder data and voltage inputs to reject noise.
49  private final KalmanFilter<N1, N1, N1> m_observer =
50      new KalmanFilter<>(
51          Nat.N1(),
52          Nat.N1(),
53          m_flywheelPlant,
54          VecBuilder.fill(3.0), // How accurate we think our model is
55          VecBuilder.fill(0.01), // How accurate we think our encoder
56          // data is
57          0.020);

 5#include <numbers>
 6
 7#include <frc/DriverStation.h>
 8#include <frc/Encoder.h>
 9#include <frc/TimedRobot.h>
10#include <frc/XboxController.h>
11#include <frc/controller/LinearQuadraticRegulator.h>
12#include <frc/drive/DifferentialDrive.h>
13#include <frc/estimator/KalmanFilter.h>
14#include <frc/motorcontrol/PWMSparkMax.h>
15#include <frc/system/LinearSystemLoop.h>
16#include <frc/system/plant/DCMotor.h>
17#include <frc/system/plant/LinearSystemId.h>
18#include <units/angular_velocity.h>

48  // The observer fuses our encoder data and voltage inputs to reject noise.
49  frc::KalmanFilter<1, 1, 1> m_observer{
50      m_flywheelPlant,
51      {3.0},   // How accurate we think our model is
52      {0.01},  // How accurate we think our encoder data is
53      20_ms};

48        # The observer fuses our encoder data and voltage inputs to reject noise.
49        self.observer = wpimath.estimator.KalmanFilter_1_1_1(
50            self.flywheelPlant,
51            [3],  # How accurate we think our model is
52            [0.01],  # How accurate we think our encoder data is
53            0.020,
54        )

Footnotes