PID’ye Giriş
Not
For a guide on implementing PID control with WPILib, see WPILib’de PID Kontrolü.
This page explains the conceptual and mathematical workings of a PID controller. A video explanation from WPI is also available.
What is a PID Controller?
The PID controller is a common feedback controller consisting of proportional, integral, and derivative terms, hence the name. This article will build up the definition of a PID controller term by term while trying to provide some intuition for how each term behaves.
First, we’ll get some nomenclature for PID controllers out of the way. In a PID context, we use the term reference or setpoint to mean the desired state of the mechanism, and the term output or process variable to refer to the measured state of the mechanism. Below are some common variable naming conventions for relevant quantities.
\(r(t)\) |
\(u(t)\) |
||
\(e(t)\) |
\(y(t)\) |
The error \(e(t)\) is the difference between the reference and the output, \(r(t) - y(t)\).
For those already familiar with PID control, this interpretation may not be consistent with the classical explanation of the P, I, and D terms corresponding to response to “past”, “present”, and “future” errors. While that model has merit, we will instead be approaching PID control from the viewpoint of modern control theory, as proportional controllers applied to different physical quantities we care about. This will provide a more complete explanation of the derivative term’s behavior for constant and moving setpoints.
Roughly speaking: the proportional term drives the position error to zero, the derivative term drives the velocity error to zero, and the integral term drives the total accumulated error-over-time to zero. All three terms are added together to produce the control signal. We’ll go into more detail on each of these below.
Not
Throughout the WPILib documentation, you’ll see two ways of writing the tunable constants of the PID controller.
For example, for the proportional gain:
\(K_p\) is the standard math-equation-focused way to notate the constant.
kPis a common way to see it written as a variable in software.
Despite the differences in capitalization, the two formats refer to the same concept.
Proportional Term - Oransal terimi
The Proportional term attempts to drive the position error to zero by contributing to the control signal proportionally to the current position error. Intuitively, this tries to move the output towards the reference.
burada \(K_p\) orantılı kazançtır ve \(e(t)\) geçerli zamandaki \(t\) hatadır.
Aşağıdaki şekil, bir P kontrolörü tarafından kontrol edilen bir system için bir blok diyagramı göstermektedir.
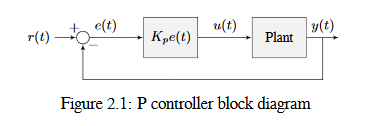
Orantılı kazançlar, system i istenen konuma çeken “yazılım tanımlı yaylar” gibi hareket eder. Fizikten şunu hatırlayın yayı modellemek için \(F = - kx\) burada \(F\) uygulanan kuvvettir, \(k\) is a orantısal bir sabit ve \(x\) denge noktasından yer değiştirmedir. Bu başka bir şekilde yazılabilir \(F = k(0-x)\) burada \(0\) denge noktasıdır. Denge noktasının geri besleme denetleyicimizin setpoint olmasına izin verirsek, denklemlerin bire bir karşılığı olur.
dolayısıyla orantısal denetleyicinin systemin output u : term:setpoint yönünde çektiği “kuvvet”, bir yay gibi error ile orantılıdır.
Derivative- Türev Terimi
The Derivative term attempts to drive the derivative of the error to zero by contributing to the control signal proportionally to the derivative of the error. Intuitively, this tries to make the output move at the same rate as the reference.
burada \(K_p\) oransal kazançtır, \(K_d\) türevsel kazançtır ve \(e(t)\) şu andaki \(t\) zamanındaki hatadır.
Aşağıdaki şekil, bir PD kontrolörü tarafından kontrol edilen bir system için bir blok diyagramı göstermektedir.
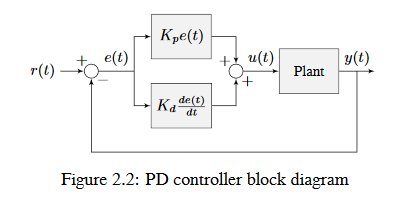
Bir PD denetleyicisinde konum için oransal bir denetleyici (\(K_p\)) ve hız için oransal denetleyici (\(K_d\)) bulunur. Hız ile ilgili setpoint , örtülü olarak pozisyon setpoint inin zaman içinde nasıl değiştiğiyle sağlanır. Bunu kanıtlamak için, bir PD kontrolörü için denklemi yeniden düzenleyeceğiz.
where \(u_k\) is the control effort at timestep \(k\) and \(e_k\) is the error at timestep \(k\). \(e_k\) is defined as \(e_k = r_k - x_k\) where \(r_k\) is the setpoint and \(x_k\) is the current state at timestep \(k\).
Nasıl olduğuna dikkat edin: \(\frac{r_k - r_{k-1}}{dt} , :term:`setpoint\) in hızıdır. Aynı nedenden ötürü, \(\frac{x_k - x_{k-1}}{dt}\), systemin belirli bir zaman adımındaki hızıdır. Bu, PD kontrol cihazının \(K_d\) teriminin, tahmini hızı setpoint hızına sürdüğü anlamına gelir.
setpoint sabitse, örtük hız setpoint sıfırdır, dolayısıyla \(K_d\) terimi system i yavaşlatır. Bu, “yazılım tanımlı bir tampon” gibi davranır. Bunlar genellikle kapı kapatıcılarda görülür ve sönümleme kuvveti hız ile doğrusal olarak artar.
İntegral Terimi
Önemli
Integral gain is generally not recommended for FRC® use. It is almost always better to use a feedforward controller to eliminate steady-state error. If you do employ integral gain, it is crucial to provide some protection against integral windup.
The Integral term attempts to drive the total accumulated error to zero by contributing to the control signal proportionally to the sum of all past errors. Intuitively, this tries to drive the average of all past output values towards the average of all past reference values.
burada \(K_p\) oransal kazanç, \(K_i\) integral kazançtır, \(e(t)\) geçerli zamandaki hatadır \(t\) ve \(\tau\) entegrasyon değişkenidir.
İntegral zaman \(0\) dan şimdiki zaman \(t\) ye kadar integral alır. Entegrasyon için \(\tau\) kullanırız çünkü integral boyunca birden fazla değeri alacak bir değişkene ihtiyacımız vardır, ancak şunu kullanamayız \(t\) çünkü bunu şimdiki zaman olarak tanımlamıştık.
Aşağıdaki şekil, bir PI kontrolörü tarafından kontrol edilen bir system için bir blok diyagramı gösterir.
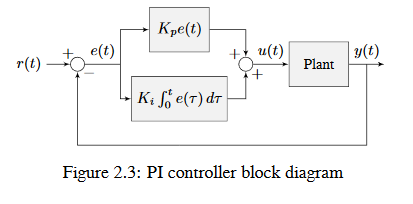
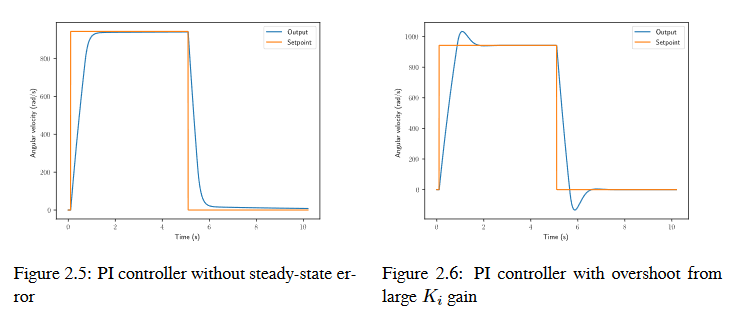
system kararlı durumda setpoint i kapattığında, oransal terim output u :terim:`setpoint` na çekmek için çok küçük olabilir, ve türev terimi sıfırdır. Bu, şekil 2.4’te gösterildiği gibi steady-state error ile sonuçlanabilir.
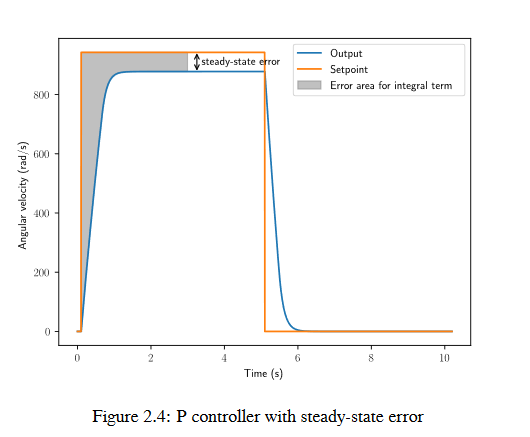
A common way of eliminating steady-state error is to integrate the error and add it to the control effort. This increases the control effort until the system converges. Figure 2.4 shows an example of steady-state error for a flywheel, and figure 2.5 shows how an integrator added to the flywheel controller eliminates it. However, too high of an integral gain can lead to overshoot, as shown in figure 2.6.
Putting It All Together
Not
WPILib tarafından sağlanan PIDController’ı kullanma hakkında bilgi için bkz ilgili makale.
When these terms are combined by summing them all together, one gets the typical definition for a PID controller.
burada \(K_p\) oransal kazançtır, \(K_i\) integral kazançtır, \(K_d\) türevsel kazançtır, \(e(t)\) şu andaki hatadır \(t\) ve \(\tau\) entegrasyon değişkenidir.
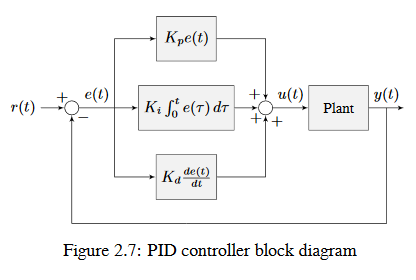
Aşağıdaki şekil, bir PID kontrolörü için bir blok diyagramı göstermektedir.
Yanıt Türleri
PID denetleyicisi tarafından çalıştırılan system genellikle üç tür yanıt içerir: yetersiz sönümlü, aşırı sönümlü ve kritik sönümlü. Bunlar şekil 2.8’de gösterilmektedir.
Resim 2.7 de step responses için; rise time, system`in :term:`step input`u uyguladıktan sonra referansa ulaşmaya başlaması için gereken zamandır. :term:`Settling time:term:`system`in :term:`step input`u uyguladıktan sonra :term:`reference`a oturmaya başlaması için gereken zamandır.
Yetersiz sönümlenmiş-underdamped bir yanıt, oturmadan önce reference etrafında salınır. Aşırı sönümlenmiş-overdamped bir yanıt
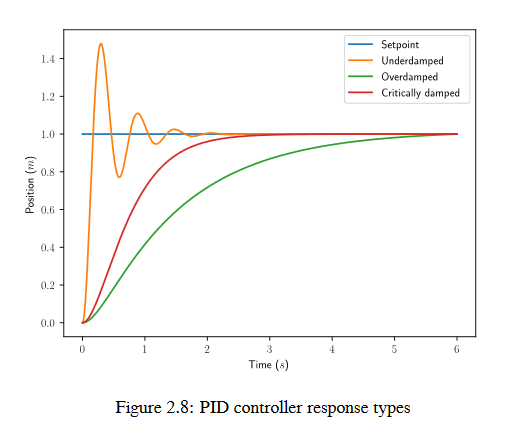
yavaş yükselir ve reference yi aşmaz. Kritik olarak sönümlenen-critically damped bir yanıt, reference öğesini aşmadan en hızlı rise time a sahipdir.