State-Space Kontrolörü Çözüm Yolu

Not

Bu öğreticiyi izlemeden önce, okuyucuların bir durum-uzay kontrolüne girişi okumaları önerilir Durum Uzayı - State-space Kontrolüne Giriş

Bu öğreticinin amacı, bir volan için bir durum-uzay kontrolörünün uygulanmasına ilişkin “uçtan uca” talimatlar sağlamaktır. Bu öğreticiyi takip ederek okuyucular şunları öğreneceklerdir:

1. Create an accurate state-space model of a flywheel using system identification or CAD software.

2. Enkoder hızı ölçümlerini gecikmeden filtrelemek için bir Kalman Filtresi uygulayın.

3. Bir LQR geri besleme denetleyicisi uygulayın; bu, model tabanlı ileri besleme ile birleştirildiğinde, çarkı a reference “referans” a sürmek için voltaj inputs oluşturur.

Bu öğretici, çok fazla programlama uzmanlığı olmayan ekipler için ulaşılabilir olması amaçlanmıştır. WPILib kitaplığı, durum-uzay kontrol özelliklerinin uygulanma biçiminde önemli bir esneklik sunarken, bu eğitimde ana hatları verilen uygulamayı yakından takip etmek, ekiplere çeşitli durum-uzay sistemleri için yeniden kullanılabilecek temel bir yapı sağlamalıdır.

The full example is available in the state-space flywheel (Java/C++/Python) and state-space flywheel system identification (Java/C++/Python) example projects.

State-Space Control-Durum Uzayı Kontrolü Neden Kullanılır?

State-Space Control-Durum-uzay kontrolü, sistemimizin doğru bir modelini oluşturmaya odaklandığından, model will respond to control inputs 1 e nasıl tepki vereceğini doğru bir şekilde tahmin edebiliriz. Bu, mekanizmalarımızı fiziksel bir robota erişim olmadan simüle etmemize ve aynı zamanda kolayca seçim yapmamıza olanak tanır gains iyi çalışacağını bildiğimiz kazançlardır. Bir modele sahip olmak, sensör okumalarını en iyi şekilde filtrelemek için Kalman Filtreleri gibi gecikmesiz filtreler oluşturmamıza da olanak tanır.

Flywheel-Volanımızın Modellenmesi

Recall that continuous state-space systems are modeled using the following system of equations:

\[\begin{split}\dot{\mathbf{x}} &= \mathbf{A}\mathbf{x} + \mathbf{B}\mathbf{u} \\ \mathbf{y} &= \mathbf{C}\mathbf{x} + \mathbf{D}\mathbf{u}\end{split}\]

Where x-dot is the rate of change of the system’s state, \(\mathbf{x}\) is the system’s current state, \(\mathbf{u}\) is the input to the system, and \(\mathbf{y}\) is the system’s output.

Let’s use this system of equations to model our flywheel in two different ways. We’ll first model it using system identification using the SysId toolsuite, and then model it based on the motor and flywheel’s moment of inertia.

Durum uzayı sistemimizi oluşturmanın ilk adımı, sistemimizin durumlarını seçmektir. Devlet olarak istediğimiz her şeyi seçebiliriz - istersek tamamen ilgisiz durumları seçebiliriz - ama önemli olan durumları seçmeye yardımcı olur. Bizim durumumuzdaki hidden states ifadesini dahil edebiliriz (sadece konumunu ölçebilseydik asansör hızı gibi) ve Kalman Filtremizin değerlerini tahmin etmesine izin verebiliriz. Seçtiğimiz durumların, geribildirim denetleyicisi tarafından ilgili references e doğru yönlendirileceğini unutmayın (tipik olarak : ref:` Doğrusal Karesel Düzenleyici <docs/software/advanced-controls/state-space/state-space-intro:The Linear-Quadratic Regulator>`, çünkü optimaldir).

Volanımız için yalnızca tek bir durumu önemsiyoruz : hızı. İvmesini de modellemeyi seçebilirken, bu durumun dahil edilmesi sistemimiz için gerekli değildir.

Daha sonra, : terimini tanımlıyoruz: `sistemimize <input> girişleri. Girdiler, durumunu değiştirmek için sistemimize “into-içine” koyabileceğimiz şeyler olarak düşünülebilir. Volan (ve FRC ® ‘deki diğer birçok tek eklemli mekanizma) durumunda, sadece bir girişimiz var: motora uygulanan voltaj. Girişimiz olarak voltajı seçerek (motor görev döngüsü gibi bir şey üzerinde), akü yükü arttıkça akü voltajındaki düşüşü telafi edebiliriz.

Sürekli zaman durum-uzay sistemi şunu yazar x-dot veya sistemin system' durumunun anlık değişim oranı, şu anki state ile orantılı olarak ve inputs<input>’. Durumumuz açısal hız olduğundan, :math:mathbf{dot{x}}` volanın açısal ivmesi olacaktır.

Daha sonra, çarkımızı sürekli zaman durum-uzay sistemi olarak modelleyeceğiz. WPILib’in LinearSystem’ sistemi bunu dahili olarak ayrık zamana dönüştürecektir. Gözden geçirme : ref: “durum uzayı gösterimi <docs/software/advanced-controls/state-space/state-space-intro:What is State-Space Notation?>``, sürekli zamanlı ve ayrık zamanlı sistemler hakkında daha fazla bilgi için.

Sistem Tanımlama ile Modelleme

To rewrite this in state-space notation using system identification, we recall from the flywheel state-space notation example, where we rewrote the following equation in terms of \(\mathbf{a}\).

\[\begin{split}V = kV \cdot \mathbf{v} + kA \cdot \mathbf{a}\\ \mathbf{a} = \mathbf{\dot{v}} = \begin{bmatrix}\frac{-kV}{kA}\end{bmatrix} v + \begin{bmatrix}\frac{1}{kA}\end{bmatrix} V\end{split}\]

Burada:math:mathbf{v} , volan hızıdır,:math:mathbf{a} ve:math:mathbf{dot{v}}, volan ivmesidir ve \(V\) voltajdır. Bunu, durum vektörü için standart \(\mathbf{x}\) ve giriş vektörü için : math:mathbf {u} standart kuralıyla yeniden yazarak şunu buluruz:

\[\mathbf{\dot{x}} = \begin{bmatrix}\frac{-kV}{kA} \end{bmatrix} \mathbf{x} + \begin{bmatrix}\frac{1}{kA} \end{bmatrix} \mathbf{u}\]

Durum uzayı notasyonunun ikinci bölümü, sistemin o anki :term:state ve girdileri ile output ile ilişkilidir. Bir volan durumunda, çıktı vektörümüz \(\mathbf{y}\) (veya sensörlerimizin ölçebildiği şeyler) volanımızın hızıdır ve bu da bizim state \(\mathbf{x}\) vektörümüzün bir unsuru olur . Bu nedenle, çıktı matrisimiz \(\mathbf{C} = \begin{bmatrix}1 \end{bmatrix}\) ve sistem besleme matrisimiz \(\mathbf{D} = \begin{bmatrix}0 \end{bmatrix}\) olur. Bunu sürekli zaman durum uzayı gösteriminde yazmak aşağıdakileri verir.

\[\begin{split}\mathbf{\dot{x}} &= \begin{bmatrix}\frac{-kV}{kA} \end{bmatrix} \mathbf{x} + \begin{bmatrix}\frac{1}{kA} \end{bmatrix} \mathbf{u} \\ \mathbf{y} &= \begin{bmatrix}1\end{bmatrix} \mathbf{x} + \begin{bmatrix}0\end{bmatrix} \mathbf{u}\end{split}\]

LinearSystem sınıfı, şu şekilde tanımlanmış durum uzayı sistemlerini kolayca oluşturmak için yöntemler içerir system identification. Bu örnek, kV değeri 0,023 ve kA değeri 0,001 olan bir volan modelini göstermektedir:

Java

  // Volts per (radian per second)
  private static final double kFlywheelKv = 0.023;

  // Volts per (radian per second squared)
  private static final double kFlywheelKa = 0.001;

  // The plant holds a state-space model of our flywheel. This system has the following properties:
  //
  // States: [velocity], in radians per second.
  // Inputs (what we can "put in"): [voltage], in volts.
  // Outputs (what we can measure): [velocity], in radians per second.
  //
  // The Kv and Ka constants are found using the FRC Characterization toolsuite.
  private final LinearSystem<N1, N1, N1> m_flywheelPlant =
      LinearSystemId.identifyVelocitySystem(kFlywheelKv, kFlywheelKa);

C++

#include <frc/system/plant/LinearSystemId.h>

  // Volts per (radian per second)
  static constexpr auto kFlywheelKv = 0.023_V / 1_rad_per_s;

  // Volts per (radian per second squared)
  static constexpr auto kFlywheelKa = 0.001_V / 1_rad_per_s_sq;

  // The plant holds a state-space model of our flywheel. This system has the
  // following properties:
  //
  // States: [velocity], in radians per second.
  // Inputs (what we can "put in"): [voltage], in volts.
  // Outputs (what we can measure): [velocity], in radians per second.
  //
  // The Kv and Ka constants are found using the FRC Characterization toolsuite.
  frc::LinearSystem<1, 1, 1> m_flywheelPlant =
      frc::LinearSystemId::IdentifyVelocitySystem<units::radian>(kFlywheelKv,
                                                                 kFlywheelKa);

Python

# Volts per (radian per second)
kFlywheelKv = 0.023

# Volts per (radian per second squared)
kFlywheelKa = 0.001

        # The plant holds a state-space model of our flywheel. This system has the following properties:
        #
        # States: [velocity], in radians per second.
        # Inputs (what we can "put in"): [voltage], in volts.
        # Outputs (what we can measure): [velocity], in radians per second.
        #
        # The Kv and Ka constants are found using the FRC Characterization toolsuite.
        self.flywheelPlant = (
            wpimath.system.plant.LinearSystemId.identifyVelocitySystemRadians(
                kFlywheelKv, kFlywheelKa
            )
        )

Volan Atalet Momenti ve Dişli Kullanarak Modelleme

A flywheel can also be modeled without access to a physical robot, using information about the motors, gearing and flywheel’s moment of inertia. A full derivation of this model is presented in Section 12.3 of Controls Engineering in FRC.

The LinearSystem class contains methods to easily create a model of a flywheel from the flywheel’s motors, gearing and moment of inertia. The moment of inertia can be calculated using CAD software or using physics. The examples used here are detailed in the flywheel example project (Java/C++/Python).

Not

WPILib’in durum uzayı sınıfları için dişli, giriş üzerinden çıkış olarak yazılır - yani, volan motorlardan daha yavaş dönüyorsa, bu sayı birden büyük olmalıdır.

Not

C ++ LinearSystem sınıfı, birim karışıklıklarını önlemek ve boyutluluğu ileri sürmek için the C++ Units Library kullanır.

Java

  private static final double kFlywheelMomentOfInertia = 0.00032; // kg * m^2

  // Reduction between motors and encoder, as output over input. If the flywheel spins slower than
  // the motors, this number should be greater than one.
  private static final double kFlywheelGearing = 1.0;

  // The plant holds a state-space model of our flywheel. This system has the following properties:
  //
  // States: [velocity], in radians per second.
  // Inputs (what we can "put in"): [voltage], in volts.
  // Outputs (what we can measure): [velocity], in radians per second.
  private final LinearSystem<N1, N1, N1> m_flywheelPlant =
      LinearSystemId.createFlywheelSystem(
          DCMotor.getNEO(2), kFlywheelMomentOfInertia, kFlywheelGearing);

C++

#include <frc/system/plant/LinearSystemId.h>

#include <frc/system/plant/LinearSystemId.h>
  static constexpr units::kilogram_square_meter_t kFlywheelMomentOfInertia =
      0.00032_kg_sq_m;

  // Reduction between motors and encoder, as output over input. If the flywheel
  // spins slower than the motors, this number should be greater than one.
  static constexpr double kFlywheelGearing = 1.0;

  // The plant holds a state-space model of our flywheel. This system has the
  // following properties:
  //
  // States: [velocity], in radians per second.
  // Inputs (what we can "put in"): [voltage], in volts.
  // Outputs (what we can measure): [velocity], in radians per second.
  frc::LinearSystem<1, 1, 1> m_flywheelPlant =
      frc::LinearSystemId::FlywheelSystem(
          frc::DCMotor::NEO(2), kFlywheelMomentOfInertia, kFlywheelGearing);

Python

kFlywheelMomentOfInertia = 0.00032  # kg/m^2

# Reduction between motors and encoder, as output over input. If the flywheel spins slower than
# the motors, this number should be greater than one.
kFlywheelGearing = 1

        # The plant holds a state-space model of our flywheel. This system has the following properties:
        #
        # States: [velocity], in radians per second.
        # Inputs (what we can "put in"): [voltage], in volts.
        # Outputs (what we can measure): [velocity], in radians per second.
        self.flywheelPlant = wpimath.system.plant.LinearSystemId.flywheelSystem(
            wpimath.system.plant.DCMotor.NEO(2),
            kFlywheelMomentOfInertia,
            kFlywheelGearing,
        )

Kalman Filtreleri: Volan Durumunu Gözlemleme

Kalman filtreleri, bir durum tahmini oluşturmak için durum uzayı modelimizi kullanarak hız ölçümlerimizi filtrelemek için kullanılır : math:mathbf {hat {x}}. Volan modelimiz doğrusal olduğundan, volanın hızını tahmin etmek için bir Kalman filtresi kullanabiliriz. WPILib’in Kalman filtresi, model ve sensör ölçümlerinin standart sapmalarıyla birlikte bir LinearSystem (yukarıda bulduğumuz) alır. Bu ağırlıkları ayarlayarak durum tahminimizin ne kadar “smooth-düzgün” olduğunu ayarlayabiliriz. Daha büyük durum standart sapmaları, filtrenin durumumuza “distrust-güvenmemesine” ve yeni ölçümleri daha fazla tercih etmesine neden olurken, daha büyük ölçüm standart sapmaları bunun tersini yapacaktır.

Bir volan durumunda, 3 rad / s’lik bir durum standart sapması ve 0.01 rad / s’lik bir ölçüm standardı sapması ile başlarız. Bu değerler kullanıcının seçmesine bağlıdır - bu ağırlıklar bir miktar gürültüye toleranslı olan ancak durum tahmini a volan için dış parazitlere hızlı bir şekilde tepki veren bir filtre üretti ve aşağıdakiler için iyi davranan bir filtre oluşturmak için ayarlanmalıdır. özel volanınız. Zaman içindeki durumları, ölçümleri, girdileri, referansları ve çıktıları grafiklemek, Kalman filtrelerini ayarlamak için harika bir görsel yoldur.

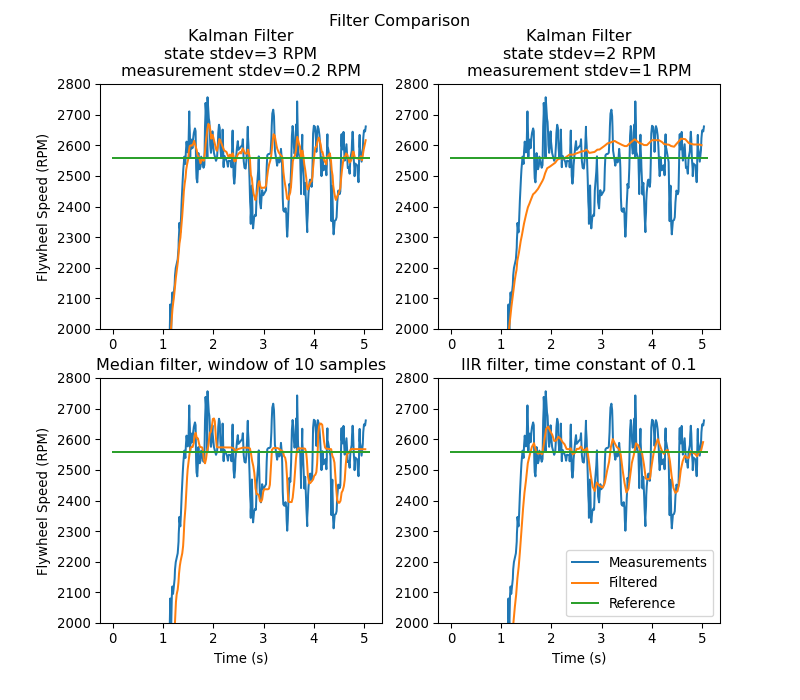
Yukarıdaki grafik, iki farklı şekilde ayarlanmış Kalman filtresinin yanı sıra bir:single-pole IIR filter ve Median Filtresi gösterir. Bu veriler, bir atıcı ile ~ 5 saniyede toplandı ve dört top, atıcıdan geçirildi (hızdaki dört düşüşte görüldüğü gibi). İyi durum ve ölçüm standardı sapmalarını seçme konusunda katı kurallar olmamakla birlikte, bunlar genel olarak, harici rahatsızlıklara hızlı tepki verirken gürültüyü reddedecek kadar modele güvenecek şekilde ayarlanmalıdır.

Because the feedback controller computes error using the x-hat estimated by the Kalman filter, the controller will react to disturbances only as quickly the filter’s state estimate changes. In the above chart, the upper left plot (with a state standard deviation of 3.0 and measurement standard deviation of 0.2) produced a filter that reacted quickly to disturbances while rejecting noise, while the upper right plot shows a filter that was barely affected by the velocity dips.

Java

  // The observer fuses our encoder data and voltage inputs to reject noise.
  private final KalmanFilter<N1, N1, N1> m_observer =
      new KalmanFilter<>(
          Nat.N1(),
          Nat.N1(),
          m_flywheelPlant,
          VecBuilder.fill(3.0), // How accurate we think our model is
          VecBuilder.fill(0.01), // How accurate we think our encoder
          // data is
          0.020);

C++

#include <frc/estimator/KalmanFilter.h>

  // The observer fuses our encoder data and voltage inputs to reject noise.
  frc::KalmanFilter<1, 1, 1> m_observer{
      m_flywheelPlant,
      {3.0},   // How accurate we think our model is
      {0.01},  // How accurate we think our encoder data is
      20_ms};

Python

        # The observer fuses our encoder data and voltage inputs to reject noise.
        self.observer = wpimath.estimator.KalmanFilter_1_1_1(
            self.flywheelPlant,
            [3],  # How accurate we think our model is
            [0.01],  # How accurate we think our encoder data is
            0.020,
        )

Kalman filtreleri : ref: docs / software / advanced-controls / state-space / state-space-observers: Predict step’de durum uzayı modelimizi kullandığından, modelimizin mümkün olduğu kadar doğru olması önemlidir. Bunu doğrulamanın bir yolu, bir volanın giriş voltajını ve zaman içindeki hızını kaydetmek ve bu verileri Kalman filtresinde yalnızca predict-tahmin olarak adlandırarak yeniden yürütmektir. Daha sonra, kV ve kA kazançları (veya eylemsizlik momenti ve diğer sabitler), model kaydedilen verilerle yakından eşleşene kadar ayarlanabilir.

Doğrusal-Kuadratik Düzenleyiciler ve Plant Inversion Feedforward-İleri Besleme

Linear-Quadratic Regulator / Doğrusal-Kuadratik Düzenleyici, volanımızı system i reference a sürmek için bir geri bildirim denetleyicisi bulur . Volanımızın sadece bir durumu olduğu için, LQR’miz tarafından seçilen kontrol yasası şu biçimde olacaktır \(\mathbf{u = K (r - x)}\) burada \(\mathbf{K}\), bir 1x1 matrisdir; başka bir deyişle, LQR tarafından seçilen kontrol kuralı basitçe orantılı bir kontrolör veya sadece bir P kazancı olan bir PID kontrolörüdür. Bu kazanç, LQR’miz tarafından, geçtiğimiz durum gezi ve kontrol çabalarına göre seçilir. LQR denetleyicilerinin ayarlanması hakkında daha fazla bilgi şu adreste bulunabilir LQR uygulama örneği.

SimpleMotorFeedforward gibi, kS, kV ve kA sabitleri verilen ileri besleme voltaj girişleri oluşturmak için kullanılabilir, Plant Inversion Feedforward sınıfı, bir durum uzay sistemi verilen feedforward voltaj girişlerini üretir. `` LinearSystemLoop`` sınıfı tarafından üretilen gerilim komutları ileri besleme ve geri besleme girişlerinin toplamıdır.

Java

  // A LQR uses feedback to create voltage commands.
  private final LinearQuadraticRegulator<N1, N1, N1> m_controller =
      new LinearQuadraticRegulator<>(
          m_flywheelPlant,
          VecBuilder.fill(8.0), // qelms. Velocity error tolerance, in radians per second. Decrease
          // this to more heavily penalize state excursion, or make the controller behave more
          // aggressively.
          VecBuilder.fill(12.0), // relms. Control effort (voltage) tolerance. Decrease this to more
          // heavily penalize control effort, or make the controller less aggressive. 12 is a good
          // starting point because that is the (approximate) maximum voltage of a battery.
          0.020); // Nominal time between loops. 0.020 for TimedRobot, but can be
  // lower if using notifiers.

C++

#include <frc/controller/LinearQuadraticRegulator.h>

  // A LQR uses feedback to create voltage commands.
  frc::LinearQuadraticRegulator<1, 1> m_controller{
      m_flywheelPlant,
      // qelms. Velocity error tolerance, in radians per second. Decrease this
      // to more heavily penalize state excursion, or make the controller behave
      // more aggressively.
      {8.0},
      // relms. Control effort (voltage) tolerance. Decrease this to more
      // heavily penalize control effort, or make the controller less
      // aggressive. 12 is a good starting point because that is the
      // (approximate) maximum voltage of a battery.
      {12.0},
      // Nominal time between loops. 20ms for TimedRobot, but can be lower if
      // using notifiers.
      20_ms};

  // The state-space loop combines a controller, observer, feedforward and plant
  // for easy control.
  frc::LinearSystemLoop<1, 1, 1> m_loop{m_flywheelPlant, m_controller,
                                        m_observer, 12_V, 20_ms};

Python

        # A LQR uses feedback to create voltage commands.
        self.controller = wpimath.controller.LinearQuadraticRegulator_1_1(
            self.flywheelPlant,
            [8],  # qelms. Velocity error tolerance, in radians per second. Decrease
            # this to more heavily penalize state excursion, or make the controller behave more
            # aggressively.
            [12],  # relms. Control effort (voltage) tolerance. Decrease this to more
            # heavily penalize control effort, or make the controller less aggressive. 12 is a good
            # starting point because that is the (approximate) maximum voltage of a battery.
            0.020,  # Nominal time between loops. 0.020 for TimedRobot, but can be lower if using notifiers.
        )

Hepsini Bir Araya Getirin : LinearSystemLoop

LinearSystemLoop, daha önce oluşturduğumuz sistemimizi, denetleyicimizi ve gözlemcimizi birleştirir. Gösterilen kurucu ayrıca bir PlantInversionFeedforward başlatacaktır.

Java

  // The state-space loop combines a controller, observer, feedforward and plant for easy control.
  private final LinearSystemLoop<N1, N1, N1> m_loop =
      new LinearSystemLoop<>(m_flywheelPlant, m_controller, m_observer, 12.0, 0.020);

C++

#include <frc/system/LinearSystemLoop.h>

  // The state-space loop combines a controller, observer, feedforward and plant
  // for easy control.
  frc::LinearSystemLoop<1, 1, 1> m_loop{m_flywheelPlant, m_controller,
                                        m_observer, 12_V, 20_ms};

Python

        # The state-space loop combines a controller, observer, feedforward and plant for easy control.
        self.loop = wpimath.system.LinearSystemLoop_1_1_1(
            self.flywheelPlant, self.controller, self.observer, 12.0, 0.020
        )

LinearSystemLoop umuza sahip olduğumuzda, geriye kalan tek şey onu çalıştırmaktır. Bunu yapmak için, Kalman filtremizi yeni enkoder hız ölçümlerimizle periyodik olarak güncelleyeceğiz ve ona yeni voltaj komutları uygulayacağız. Bunu yapmak için, önce reference yi, ardından mevcut volan hızıyla correct`, bir sonraki zaman adımına Kalman filtresini predict ve getU kullanılarak oluşturulan girdileri uyguluyoruz. .

Java

  @Override
  public void teleopPeriodic() {
    // Sets the target speed of our flywheel. This is similar to setting the setpoint of a
    // PID controller.
    if (m_joystick.getTriggerPressed()) {
      // We just pressed the trigger, so let's set our next reference
      m_loop.setNextR(VecBuilder.fill(kSpinupRadPerSec));
    } else if (m_joystick.getTriggerReleased()) {
      // We just released the trigger, so let's spin down
      m_loop.setNextR(VecBuilder.fill(0.0));
    }

    // Correct our Kalman filter's state vector estimate with encoder data.
    m_loop.correct(VecBuilder.fill(m_encoder.getRate()));

    // Update our LQR to generate new voltage commands and use the voltages to predict the next
    // state with out Kalman filter.
    m_loop.predict(0.020);

    // Send the new calculated voltage to the motors.
    // voltage = duty cycle * battery voltage, so
    // duty cycle = voltage / battery voltage
    double nextVoltage = m_loop.getU(0);
    m_motor.setVoltage(nextVoltage);
  }
}

C++

#include <numbers>

#include <frc/DriverStation.h>
#include <frc/Encoder.h>
#include <frc/TimedRobot.h>
#include <frc/XboxController.h>
#include <frc/controller/LinearQuadraticRegulator.h>
#include <frc/drive/DifferentialDrive.h>
#include <frc/estimator/KalmanFilter.h>
#include <frc/motorcontrol/PWMSparkMax.h>
#include <frc/system/LinearSystemLoop.h>
#include <frc/system/plant/DCMotor.h>
#include <frc/system/plant/LinearSystemId.h>

  void TeleopPeriodic() override {
    // Sets the target speed of our flywheel. This is similar to setting the
    // setpoint of a PID controller.
    if (m_joystick.GetRightBumper()) {
      // We pressed the bumper, so let's set our next reference
      m_loop.SetNextR(frc::Vectord<1>{kSpinup.value()});
    } else {
      // We released the bumper, so let's spin down
      m_loop.SetNextR(frc::Vectord<1>{0.0});
    }

    // Correct our Kalman filter's state vector estimate with encoder data.
    m_loop.Correct(frc::Vectord<1>{m_encoder.GetRate()});

    // Update our LQR to generate new voltage commands and use the voltages to
    // predict the next state with out Kalman filter.
    m_loop.Predict(20_ms);

    // Send the new calculated voltage to the motors.
    // voltage = duty cycle * battery voltage, so
    // duty cycle = voltage / battery voltage
    m_motor.SetVoltage(units::volt_t{m_loop.U(0)});
  }

Python

    def teleopPeriodic(self) -> None:
        # Sets the target speed of our flywheel. This is similar to setting the setpoint of a
        # PID controller.
        if self.joystick.getTriggerPressed():
            # We just pressed the trigger, so let's set our next reference
            self.loop.setNextR([kSpinUpRadPerSec])

        elif self.joystick.getTriggerReleased():
            # We just released the trigger, so let's spin down
            self.loop.setNextR([0.0])

        # Correct our Kalman filter's state vector estimate with encoder data.
        self.loop.correct([self.encoder.getRate()])

        # Update our LQR to generate new voltage commands and use the voltages to predict the next
        # state with out Kalman filter.
        self.loop.predict(0.020)

        # Send the new calculated voltage to the motors.
        # voltage = duty cycle * battery voltage, so
        # duty cycle = voltage / battery voltage
        nextVoltage = self.loop.U()
        self.motor.setVoltage(nextVoltage)

Angle Wrap with LQR

Mechanisms with a continuous angle can have that angle wrapped by calling the code below instead of lqr.Calculate(x, r).

JAVA

var error = lqr.getR().minus(x);
error.set(0, 0, MathUtil.angleModulus(error.get(0, 0)));
var u = lqr.getK().times(error);

C++

Eigen::Vector<double, 2> error = lqr.R() - x;
error(0) = frc::AngleModulus(units::radian_t{error(0)}).value();
Eigen::Vector<double, 2> u = lqr.K() * error;

PYTHON

error = lqr.R() - x
error[0] = wpimath.angleModulus(error[0])
u = lqr.K() * error