מבוא ל-PID
הערה
For a guide on implementing PID control with WPILib, see בקרת PID עם WPILib.
This page explains the conceptual and mathematical workings of a PID controller. A video explanation from WPI is also available.
What is a PID Controller?
The PID controller is a common feedback controller consisting of proportional, integral, and derivative terms, hence the name. This article will build up the definition of a PID controller term by term while trying to provide some intuition for how each term behaves.
First, we’ll get some nomenclature for PID controllers out of the way. In a PID context, we use the term reference or setpoint to mean the desired state of the mechanism, and the term output or process variable to refer to the measured state of the mechanism. Below are some common variable naming conventions for relevant quantities.
\(r(t)\) |
\(u(t)\) |
||
\(e(t)\) |
\(y(t)\) |
The error \(e(t)\) is the difference between the reference and the output, \(r(t) - y(t)\).
For those already familiar with PID control, this interpretation may not be consistent with the classical explanation of the P, I, and D terms corresponding to response to ”past“, ”present“, and ”future“ errors. While that model has merit, we will instead be approaching PID control from the viewpoint of modern control theory, as proportional controllers applied to different physical quantities we care about. This will provide a more complete explanation of the derivative term’s behavior for constant and moving setpoints.
Roughly speaking: the proportional term drives the position error to zero, the derivative term drives the velocity error to zero, and the integral term drives the total accumulated error-over-time to zero. All three terms are added together to produce the control signal. We’ll go into more detail on each of these below.
הערה
Throughout the WPILib documentation, you’ll see two ways of writing the tunable constants of the PID controller.
For example, for the proportional gain:
\(K_p\) is the standard math-equation-focused way to notate the constant.
kPis a common way to see it written as a variable in software.
Despite the differences in capitalization, the two formats refer to the same concept.
קבוע פרופורציונלי
The Proportional term attempts to drive the position error to zero by contributing to the control signal proportionally to the current position error. Intuitively, this tries to move the output towards the reference.
where \(K_p\) is the proportional gain and \(e(t)\) is the error at the current time \(t\).
The below figure shows a block diagram for a system controlled by a P controller.
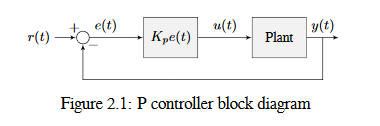
Proportional gains act like a ”software-defined springs“ that pull the system toward the desired position. Recall from physics that we model springs as \(F = - kx\) where \(F\) is the force applied, \(k\) is a proportional constant, and \(x\) is the displacement from the equilibrium point. This can be written another way as \(F = k(0-x)\) where \(0\) is the equilibrium point. If we let the equilibrium point be our feedback controller’s setpoint, the equations have a one to one correspondence.
so the ”force“ with which the proportional controller pulls the system’s output toward the setpoint is proportional to the error, just like a spring.
Derivative Term
The Derivative term attempts to drive the derivative of the error to zero by contributing to the control signal proportionally to the derivative of the error. Intuitively, this tries to make the output move at the same rate as the reference.
where \(K_p\) is the proportional gain, \(K_d\) is the derivative gain, and \(e(t)\) is the error at the current time \(t\).
The below figure shows a block diagram for a system controlled by a PD controller.

A PD controller has a proportional controller for position (\(K_p\)) and a proportional controller for velocity (\(K_d\)). The velocity setpoint is implicitly provided by how the position setpoint changes over time. To prove this, we will rearrange the equation for a PD controller.
where \(u_k\) is the control effort at timestep \(k\) and \(e_k\) is the error at timestep \(k\). \(e_k\) is defined as \(e_k = r_k - x_k\) where \(r_k\) is the setpoint and \(x_k\) is the current state at timestep \(k\).
Notice how \(\frac{r_k - r_{k-1}}{dt}\) is the velocity of the setpoint. By the same reason, \(\frac{x_k - x_{k-1}}{dt}\) is the system’s velocity at a given timestep. That means the \(K_d\) term of the PD controller is driving the estimated velocity to the setpoint velocity.
If the setpoint is constant, the implicit velocity setpoint is zero, so the \(K_d\) term slows the system down if it’s moving. This acts like a ”software-defined damper“. These are commonly seen on door closers, and their damping force increases linearly with velocity.
קבוע אינטגרלי
חשוב
Integral gain is generally not recommended for FRC® use. It is almost always better to use a feedforward controller to eliminate steady-state error. If you do employ integral gain, it is crucial to provide some protection against integral windup.
The Integral term attempts to drive the total accumulated error to zero by contributing to the control signal proportionally to the sum of all past errors. Intuitively, this tries to drive the average of all past output values towards the average of all past reference values.
where \(K_p\) is the proportional gain, \(K_i\) is the integral gain, \(e(t)\) is the error at the current time \(t\), and \(\tau\) is the integration variable.
The Integral integrates from time \(0\) to the current time \(t\). we use \(\tau\) for the integration because we need a variable to take on multiple values throughout the integral, but we can’t use \(t\) because we already defined that as the current time.
The below figure shows a block diagram for a system controlled by a PI controller.

When the system is close the setpoint in steady-state, the proportional term may be too small to pull the output all the way to the setpoint, and the derivative term is zero. This can result in steady-state error as shown in figure 2.4
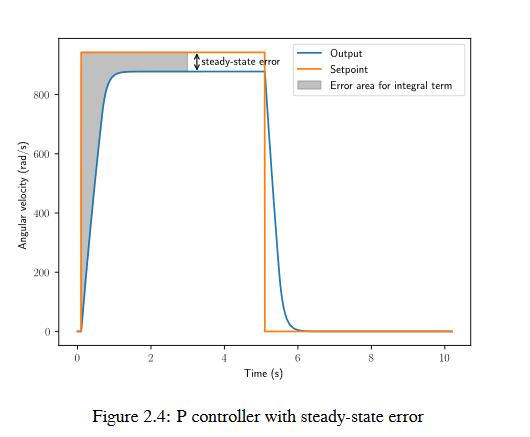
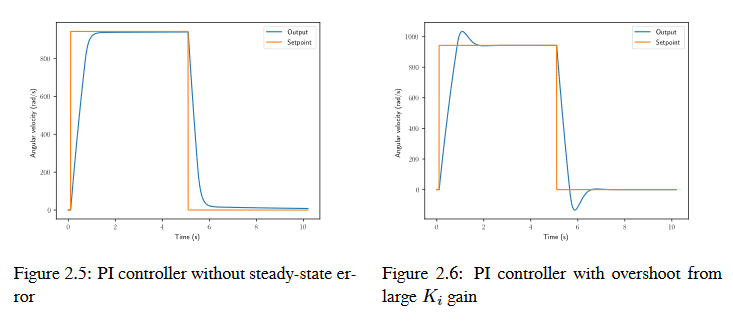
A common way of eliminating steady-state error is to integrate the error and add it to the control effort. This increases the control effort until the system converges. Figure 2.4 shows an example of steady-state error for a flywheel, and figure 2.5 shows how an integrator added to the flywheel controller eliminates it. However, too high of an integral gain can lead to overshoot, as shown in figure 2.6.
Putting It All Together
הערה
For information on using the WPILib provided PIDController, see the relevant article.
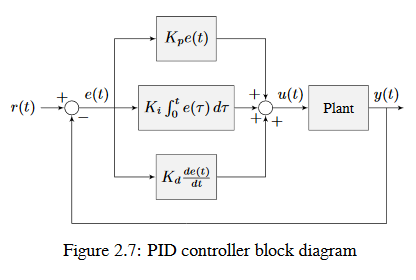
When these terms are combined by summing them all together, one gets the typical definition for a PID controller.
where \(K_p\) is the proportional gain, \(K_i\) is the integral gain, \(K_d\) is the derivative gain, \(e(t)\) is the error at the current time \(t\), and \(\tau\) is the integration variable.
The below figure shows a block diagram for a PID controller.
Response Types
A system driven by a PID controller generally has three types of responses: underdamped, over-damped, and critically damped. These are shown in figure 2.8.
For the step responses in figure 2.7, rise time is the time the system takes to initially reach the reference after applying the step input. Settling time is the time the system takes to settle at the reference after the step input is applied.
An underdamped response oscillates around the reference before settling. An overdamped response
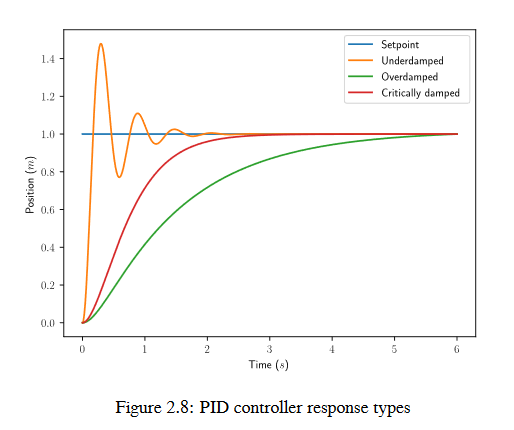
is slow to rise and does not overshoot the reference. A critically damped response has the fastest rise time without overshooting the reference.