Tuning a Vertical Arm Position Controller
In this section, we will tune a simple position controller for a vertical arm. The same tuning principles explained below will work also for almost all position-control scenarios under the load of gravity.
Arm Model Description
Vertical arms are commonly used to lift gamepieces from the ground up to a scoring position. Other similar examples include shooter hoods and elevators.
Our “vertical arm” consists of:
A mass on a stick, under the force of gravity, pivoting around an axle.
A motor and gearbox driving the axle to which the mass-on-a-stick is attached
For the purposes of this tutorial, this plant is modeled with the same equation used by WPILib’s ArmFeedforward, with additional adjustment for sensor delay and gearbox inefficiency. The simulation assumes the plant is controlled by feedforward and feedback controllers, composed in this fashion:
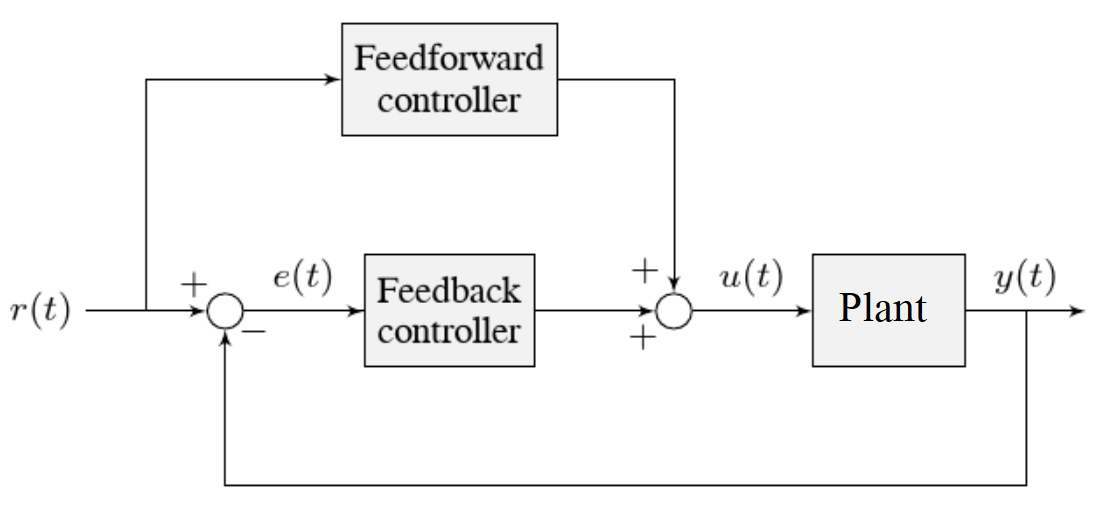
Where:
The plant’s output \(y(t)\) is the arm’s rotational position
The controller’s setpoint \(r(t)\) is the desired angle of the arm
The controller’s control effort, \(u(t)\) is the voltage applied to the motor driving the arm
Picking the Control Strategy for a Vertical Arm
Applying voltage to the motor causes a force on the mechanism that drives the arm up or down. If there is no voltage, gravity still acts on the arm to pull it downward. Generally, it is desirable to fight this effect, and keep the arm at a specific angle.
The tutorials below will demonstrate the behavior of the system under pure feedforward, pure feedback (PID), and combined feedforward-feedback control strategies. Follow the instructions to learn how to manually tune these controllers, and expand the “tuning solution” to view an optimal model-based set of tuning parameters. Even though WPILib tooling can provide you with optimal gains, it is worth going through the manual tuning process to see how the different control strategies interact with the mechanism.
Pure Feedforward Control
Interact with the simulation below to examine how the turret system responds when controlled only by a feedforward controller.
Note
To change the arm setpoint, click on the desired angle along the perimeter of the turret. To command smooth motion, click and drag the setpoint indicator.
To tune the feedforward controller, perform the following:
Set \(K_g\) and \(K_v\) to zero.
Increase \(K_g\) until the arm can hold its position with as little movement as possible. If the arm moves in the opposite direction, decrease \(K_g\) until it remains stationary. You will have to zero in on \(K_g\) fairly precisely (at least four decimal places).
Increase the velocity feedforward gain \(K_v\) until the arm tracks the setpoint during smooth, slow motion. If the arm overshoots, reduce the gain. Note that the arm may “lag” the commanded motion - this is normal, and is fine so long as it moves the correct amount in total.
Note
Feedforward-only control is not a viable control scheme for vertical arms! Do not be surprised if/when the simulation below does not behave well, even when the “correct” constants are used.
Tuning solution
The exact gains used by the simulation are \(K_g = 1.75\) and \(K_v = 1.95\).
Issues with Feed-Forward Control Alone
As mentioned above, our simulated mechanism almost-perfectly obeys the WPILib ArmFeedforward equation (as long as the “system noise” option is disabled). We might then expect, like in the case of the flywheel velocity controller, that we should be able to achieve perfect convergence-to-setpoint with a feedforward loop alone.
However, our feedforward equation relates velocity and acceleration to voltage - it allows us to control the instantaneous motion of our mechanism with high accuracy, but it does not allow us direct control over the position. This is a problem even in our simulation (in which the feedforward equation is the actual equation of motion), because unless we employ a motion profile to generate a sequence of velocity setpoints we can ask the arm to jump immediately from one position to another. This is impossible, even for our simulated arm.
The resulting behavior from the feedforward controller is to output a single “voltage spike” when the position setpoint changes (corresponding to a single loop iteration of very high velocity), and then zero voltage (because it is assumed that the system has already reached the setpoint). In practice, we can see in the simulation that this results in an initial “impulse” movement towards the target position, that stops at some indeterminate position in-between. This kind of response is called a “kick,” and is generally seen as undesirable.
You will notice that, once properly tuned, the mechanism can track slow/smooth movement with a surprising amount of accuracy - however, there are some obvious problems with this approach. Our feedforward equation corrects for the force of gravity at the setpoint - this results in poor behavior if our arm is far from the setpoint. With the “system noise” option enabled, we can also see that even smooth, slow motion eventually results in compounding position errors when only feedforward control is used. To accurately converge to and remain at the setpoint, we need to use a feedback (PID) controller.
Pure Feedback Control
Interact with the simulation below to examine how the vertical arm system responds when controlled only by a feedback (PID) controller.
Perform the following:
Set \(K_p\), \(K_i\), \(K_d\), and \(K_g\) to zero.
Increase \(K_p\) until the mechanism responds to a sudden change in setpoint by moving sharply to the new position. If the controller oscillates too much around the setpoint, reduce K_p until it stops.
Increase \(K_i\) when the output gets “stuck” before converging to the setpoint.
Increase \(K_d\) to help the system track smoothly-moving setpoints and further reduce oscillation.
Note
Feedback-only control is not a viable control scheme for vertical arms! Do not be surprised if/when the simulation below does not behave well, even when the “correct” constants are used.
Tuning solution
There is no good tuning solution for this control strategy. Values of \(K_p = 5\) and \(K_d = 1\) yield a reasonable approach to a stable equilibrium, but that equilibrium is not actually at the setpoint!
Issues with Feedback Control Alone
A set of gains that works well for one setpoint will act poorly for a different setpoint.
Adding some integral gain can push us to the setpoint over time, but it’s unstable and laggy.
Because a non-zero amount of control effort is required to keep the arm at a constant height, even when the output and setpoint are equal, this feedback-only strategy is flawed. In order to optimally control a vertical arm, a combined feedforward-feedback strategy is needed.
Combined Feedforward and Feedback Control
Interact with the simulation below to examine how the vertical arm system responds under simultaneous feedforward and feedback control.
Tuning the combined arm controller is simple - we first tune the feedforward controller following the same procedure as in the feedforward-only section, and then we tune the PID controller following the same procedure as in the feedback-only section. Notice that PID portion of the controller is much easier to tune “on top of” an accurate feedforward.
Tuning solution
Combining the feedforward coefficients from our first simulation (\(K_g = 1.75\) and \(K_v = 1.95\)) and the feedback coefficients from our second simulation (\(K_p = 5\) and \(K_d = 1\)) yields a good controller behavior.
Once tuned properly, the combined controller accurately tracks a smoothly moving setpoint, and also accurately converge to the setpoint over time after a “jump” command.
Tuning Conclusions
Choice of Control Strategies
Like in the case of the turret, and unlike the case of the flywheel, we are trying to control the position rather than the velocity of our mechanism.
In the case of the flywheel velocity controller we could achieve good control performance with feedforward alone. However, it is very hard to predict how much voltage will cause a certain total change in position (time can turn even small errors in velocity into very big errors in position). In this case, we cannot rely on feedforward control alone - as with the vertical arm, we will need a feedback controller.
Unlike in the case of the turret, though, there is a voltage required to keep the mechanism steady at the setpoint (because the arm is affected by the force of gravity). As a consequence, a pure feedback controller will not work acceptably for this system, and a combined feedforward-feedback strategy is needed.
The core reason the feedback-only control strategy fails for the vertical arm is gravity. The external force of gravity requires a constant control effort to counteract even when at rest at the setpoint, but a feedback controller does not typically output any control effort when at rest at the setpoint (unless integral gain is used, which we can see clearly in the simulation is laggy and introduces oscillations).
We saw in the feedforward-only example above that an accurate feedforward can track slow, smooth velocity setpoints quite well. Combining a feedforward controller with the feedback controller gives the smooth velocity-following of a feedforward controller with the stable long-term error elimination of a feedback controller.
Reasons for Non-Ideal Performance
This simulation does not include any motion profile generation, so acceleration setpoints are not very well-defined. Accordingly, the kA term of the feedforward equation is not used by the controller. This means there will be some amount of delay/lag inherent to the feedforward-only response.
The control law is good, but not perfect. There is usually some overshoot even for smoothly-moving setpoints - this is combination of the lack of \(K_a\) in the feedforward (see the note above for why it is omitted here), and some discretization error in the simulation. Attempting to move the setpoint too quickly can also cause the setpoint and mechanism to diverge, which (as mentioned earlier) will result in poor behavior due to the :math:’K_g’ term correcting for the wrong force, as it is calculated from the setpoint, not the measurement. Using the measurement to correct for gravity is called “feedback linearization” (as opposed to “feedforward linearization” when the setpoint is used), and can be a better control strategy if your measurements are sufficiently fast and accurate.
A Note on Feedforward and Static Friction
For the sake of simplicity, the simulations above omit the \(K_s\) term from the WPILib SimpleMotorFeedforward equation. On actual mechanisms, however, this can be important - especially if there’s a lot of friction in the mechanism gearing.
In the case of a vertical arm or elevator, \(K_s\) can be somewhat tedious to estimate separately from \(K_g\). If your arm or elevator has enough friction for \(K_s\) to be important, it is recommended that you use the WPILib system identification tool to determine your system gains.